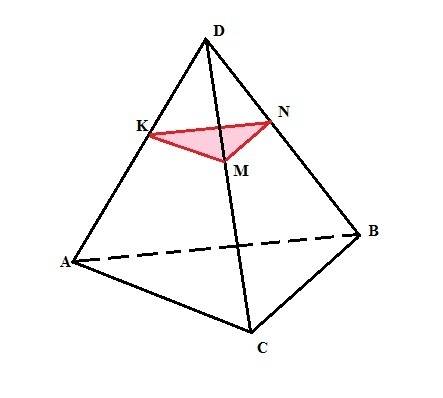
Пусть проведенное сечение пересекает ребра тетраэдра DC и DB в точках M и N соответственно. Значит сечение представляет собой треугольник KMN, параллельный треугольнику АВС и подобен ему в силу параллельности их соответственных сторон.
Рассмотрим треугольники DKM и DAC. Они подобны, так как КМ║АС. АК:КD=1:3. AK=x, тогда KD=3х. АD=AK+KD = 4x.KD/AD=3/4. Это коэффициент подобия треугольников. Итак, КМ/АС=3/4. => это коэффициент подобия треугольников KMN и АВС.
Площади подобных фигур относятся как квадрат коэффициента подобия этих фигур, то есть Skmn/Sabc=(3/4)² и Sabc=16*Skmn/9 = 16*27/9 = 48 ед².
ответ: Sabc=48 ед².
2, треугольники MNK и MPK равны по двум сторонам и углу, MK - общая, углы NMK и MKP равны, MN и KP стороны равны, а вообще это параллелограмм, там противоположные стороны и углы все равны;
8, равны по трём сторонам треугольники ABC и ADC, тут очевидно какие стороны равны;
7, MNE и NMF треугольники равны, общая сторона MN, равные углы M и N, ME и NF стороны равны.