Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
ВО:ОК=2:1
SO:ON=2:1
В равностороннем треугольнике медианы равны. Следовательно, равны и их сходственные отрезки.
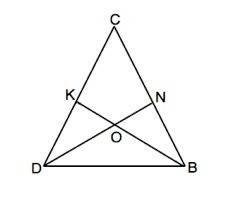
В ∆ DOK и ∆ BON равны две стороны и углы между ними при вершине О как вертикальные. Следовательно, эти треугольники равны по первому признаку.
--------
∆ DOK и ∆ BON равны и по 3-му признаку, т.к. у равных сторон равны и их половины.
А, поскольку медианы являются здесь и биссектрисами и высотами, то можно доказать их равенство и по второму признаку.
Объяснение:
ΔАВС-прямоугольный, СК⊥АВ, ∠А=69°. Тогда ∠В=90°-69°=21°.
ΔАСК-прямоугольный, ∠А=69°. Тогда ∠АСК=90°-69°=21°.
ΔВСК-прямоугольный, ∠А=21°. Тогда ∠ВСК=90°-21°=69°.
Меньший катет лежит против меньшего угла ∠В=21°, это АС.
Больший катет лежит против большего угла ∠А=69°, это ВС.
1)21°, 2)69°