1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
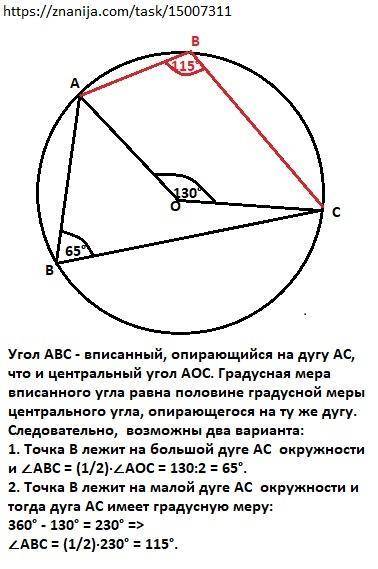
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
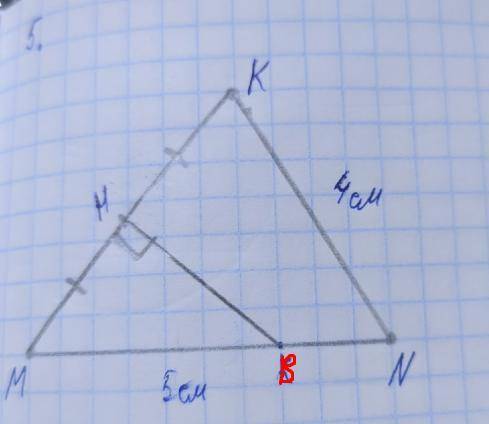
Сначала строим отрезок 5 см с линейки, затем берём транспортир, отмеряем 60 градусов (как показано на приложении ниже), ставим точку на 60-ти градусах. Далее через точку N и точку, которая указывает на 60 градусов, отмеряем отрезок 4 см с линейки. Соединяем точки M и K. Измеряем полученный отрезок (примерно 4.6 см получится). Делим полученный результат на два, отсчитываем полученное значение от любой из точек, отмечаем точку H так, что MH=MK. Затем прикладываем прямой угол к точке H, проводим прямую до пересечения с отрезком MN. HB-серединный перпендикуляр.

S=8*10/2=40
V=S*h
V=40*4=160
ответ: 160