r = (a+b-c)/2 , где а,b - катеты, с - гипотенуза, тогда
4 = (а+b -26)/2
а+b -26 = 8
а+b = 34
Таким образом Р = а+b +с =34+26 =60 (см).
2) Правило:
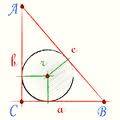
отрезки касательных к окружности, проведённые из одной точки, равны, т.е.
ВМ =ВР=5, АМ=АТ=12, СТ=СР = х, тогда по теореме Пифагора:
(5 + х)²+(12 + х)²=17²
25 + 10х + х² +144 +24х +х² = 289
2·х² +34х+169 - 289 =0
2·х² +34х -120 =0
х² + 17х -60 =0
х₁ = 3; х₂= -20 ( не подходит по смыслу задачи)
Таким образом АС = 15, ВС = 8 и Р= 15+8+17 = 40 (см).
Объяснение:
1. На прямой "а" строим угол, равный 45°. На Для этого на прямой отмечаем точку А и проводим через нее прямую "b", перпендикулярную прямой "а". Проводим полуокружность из центра А произвольного радиуса и в местах пересечения этой полуокружности с прямыми "а" и "b" отмечаем точки В и С соответственно. Соединяем точки В с С отрезком. Угол СВА равен 45°. Угол СВК равен 180 - 45 = 135° (точку К отмечаем на прямой "а" в любом месте левее точки В => углы СВК и СВА - смежные).
2. Считаем, что Вы умеете строить угол, равный данному.
Строим угол, равный 30°. Для этого проводим вертикальную прямую "а" и отмечаем на ней точку А. Из точки А как из центра проводим полуокружность до пересечения с прямой "а" в точку В. Этим же радиусом проводим полуокружность с центром в точке В и в местах пересечения полуокружностей отмечаем точки C и D. Соединяем точки А,В и С. Угол АСD равен 30°, так как треугольник АВС равносторонний, а CD - биссектриса угла АВС (CD⊥AC).
Теперь на стороне СD строим угол DCE, равный данному. То есть ∠DCE = 35°. Следовательно, ∠АСЕ = 5°.
На прямой СА строим угол FСG, равный данному углу АСЕ.
Повторяем эту процедуру 5 раз. Полученные углы ECF, FCG, GCH, HCI, ICJ, JCK и KCD равны по 5°, то есть мы разделили угол ECD на 7 равных частей.