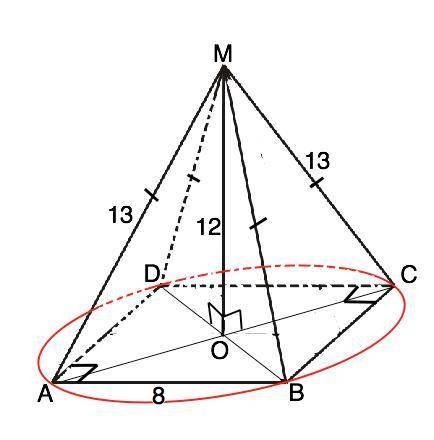
Доказательство: Назовем пирамиду МАВСD. МА=МВ=МС=МD=13, высота МО=12 и перпендикулярна основанию. Отрезки ОА=ОВ=ОС-ОD=5 ( отношения сторон из Пифагоровых троек). Треугольники МОА=МОВ=МОС=МОD по гипотенузе - (боковому ребру) и катету - высоте МО пирамиды. Поэтому равные диагонали основания - прямоугольника- являются диаметрами описанной около него окружности, а высота проецируется в центр прямоугольника, т.е в точку пересечения его диагоналей. Сторона прямоугольника 8 см оказалась для решения лишней.
1) 8 + 5 = 13 ответ: 13
2) 2*5 - 8 = 2 и 5 - 2 = 3. ответ: 3
Объяснение: СМ. изображение
1) AB - расстояние между центрами, сумма отрезков AC и BC, а они радиусы окружностей
ответ: 13
2) BD - расстояние между центрами.
AE = 10 т.к диаметр, BE = 8 как радиус большей окружности, следовательно AB = 10 - 8 = 2.
AD = 5 как радиус малой окружности. Найдем BD как разность AB и AD: BD = AD - AB = 5 - 2 = 3.
ответ: 3