ответ:Найди площадь круга, вписанного в равнобедренную трапецию с основаниями длиной 6 см и 12 см и периметром 36 см
Объяснение:
АВСМ- описанная трапеция⇒ суммы длин противоположных сторон равны. Т.е 6+12=АВ+СМ⇒ АВ=СМ=9 см. Пусть ВК⊥АМ , СР⊥АМ.
S(круга)=πr². Радиус вписанной в трапецию окружности будет равен половине высоты трапеции.
Т.к. ВК⊥АМ , СР⊥АМ, то КВСР-прямоугольник ⇒
КР=6 см, АК=РМ=(12-6) :2=3 (см).
ΔАВК-прямоугольный, по т. Пифагора :
ВК=√(9²-3²)=√((9-3)(9+3))=√(6*12)=6√2(см).
ВК-высота трапеции, значит r=3√2 см.
S(круга)= π (3√2 )²=18π (см²).
https://seoi.net/peni3d/
Практическая работа 1.
Т.к.точка О принадлежит биссекстриссе угла А,то она РАВНОУДАЛЕНА от сторон АВ и АС
Т.к.точка О принадлежит биссекстриссе угла B,то она РАВНОУДАЛЕНА от сторон BA и BС
Т.к.точка О принадлежит биссекстриссе угла C,то она РАВНОУДАЛЕНА от сторон AC и BС
Следовательно точка О равноудалена от всех сторон тругольника.Точка-это ЦЕНТР окружности.
Расстояние от т.О до любой стороны треугольника-это РАДИУС окружности.
Практическая работа 2.
Что можно сказать о взаимном расположении серединных перпендикуляров?
-все они пересекаются в т.О
Сравните OA,OB и OC.Для окружности это радиусы.
Где лежит центр вписанной окружности?На пересечении биссектрис.
чертеж к практической работе 2.
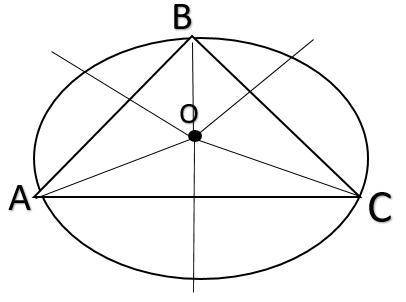
4) 45° ; 6) 67,5°
Объяснение:
4) Вписанный угол, опирающийся на дугу, равную 1/4 окружности (видно по рисунку).
∠ABC=0,5*(360° / 4)=45°
6) ∩BC - 1/4 окружности.
Точка А делит оставшуюся часть ровно пополам.
Значит, ∩АС=(360°-∩ВС) /2=270° /2=135°
И вписанный угол, опирающийся на неё, равен:
∠АВС= 1/2 * ∩АС=67,5°