Общее уравнение окружности имеет вид:
(x – a)²+(y – b)²=r²
где a и b – координаты х и у центра окружности соответственно.
Получим:
(х–3)²+(у–2)²=r²
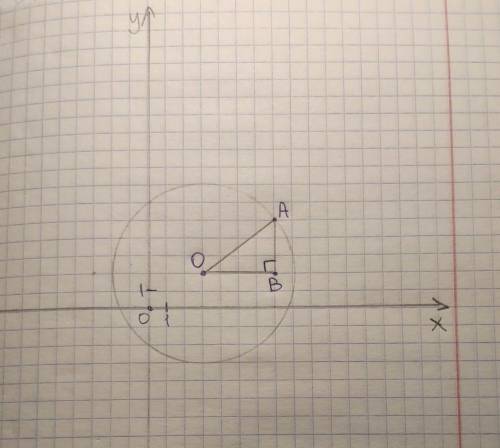
Найдем r. Радиус – это расстояние от центра (пусть это будет точка О) до любой точки на окружности (пусть данная в условии точка будет точка А)
Тогда АО=r; AO²=r².
Проведём из точки А прямую паралельную оси Оу, проведём прямую из точки О паралельную оси Ох. Точка пересечения будет точка В.
Так как кординатные оси перпендикулярны, тоесть образуют угол в 90°, то угол АВО так же будет равен 90°. Тогда ∆АВО – прямоугольный.
В прямоугольном треугольнике АВО по теореме Пифагора:
АО²=АВ²+ВО²
АО²=(5–2)²+(7–3)²
АО²=9+16
АО²=25
Тогда получим:
(х–3)²+(у–2)²=25
ответ: (х–3)²+(у–2)²=25
Үшбұрыштың теңдік белгілері.
1. Егер бірінші үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы екінші үшбұрыштың сәйкес екі қабырғасы мен арасындағы бұрышқа тең болса, онда бұл үшбұрыштар тең болады.
2. Егер бірінші үшбұрыштың бір қабырғасы және оған іргелес жатқан екі бұрышы екінші үшбұрыштың сәйкес қабырғасы мен оған іргелес жатқан екі бұрышына тең болса, онда бұл үшбұрыштар тең болады.
3. Егер бір үшбұрыштың үш қабырғасы екінші үшбұрыштың сәйкес үш қабырғасына тең болса, онда бұл үшбұрыштар тең болады.
Объяснение:
Сделаем построение по условию.
Пусть боковая сторона АС=а
На основании данных (Площадь треугольника АВС равна 9√2, угол А = 45 градусов. )
Площадь по формуле S=1/2*a^2*sinA
Получаем квадрат боковой стороны АС^2=а^2= 2S/sinA
Пусть прямая, проходящая через точку О и середину АС пересекает АС в точке К АК=КС , тогда ОК – серединный перпендикуляр , проведенный к хорде АС
Рассмотрим треугольник АМК . Углы АКМ=90 КАМ=45 АМК=45(180-90-45)
Т.е. треугольник АМК . прямоугольный, равнобедренный
Тогда АК=МК = 1/2АС МК –высота в треугольнике АМС
Площадь треугольника S(АМС)=1/2*МК*АС=1/2*(1/2АС)*АС=1/4*АС^2=1/4*a^2=1/4*2S/sinA =
=1/4*2*9√2/sin45=1/4*2*9√2/(√2/2) = 9
Тогда площадь треугольника S(ВМС)=S(ABC)-S(AMC)= 9√2-9=9(1-√2)
***возможна другая форма ответа