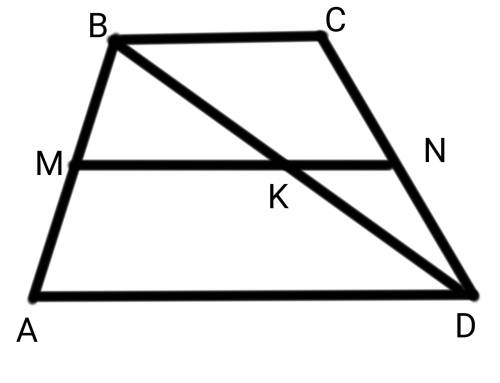
AD=20, BC=6, BM=AM, CN=ND.
Теорема Фалеса гласит, что если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
То есть, так как CN=ND и BC||KN, отрезки BK и KD равны.
Следовательно KN средняя линия треугольника BCD. А средняя линия треугольника равна половине параллельной стороны. Параллельная сторона KN это BC. BC=6, поэтому KN=6/2=3. Меньший отрезок равен 3.
По тем же свойствам, что и сверху MK средняя линия треугольника ABD и равна половине AD. AD=20.
MK=20/2=10
Больший отрезок равен 10
Думаю, Вы без труда справились бы с задачами самостоятельно, если бы сделали рисунки к ним.
Трапеция :
Треугольник примыкает к стороне АВ. Его сторона ВЕ=СД
Значит, от периметра трапеции периметр треугольника отличается на длину двух ВС ( в параллелограмме ВСДЕ - ЕД=ВС)
Периметр трапеции равен 12+6·2=24 см (длина АЕ дана, видимо, чтобы слегка запутать)
Ромб, в котором тупой угол равен 120 градусам, "составлен" из двух равносторонних треугольников. Меньшая диагональ в нем равна стороне ромба. ⇒
Сторона ромба 8 см, периметр 4·8=32 см
ответ:вот
Объяснение: