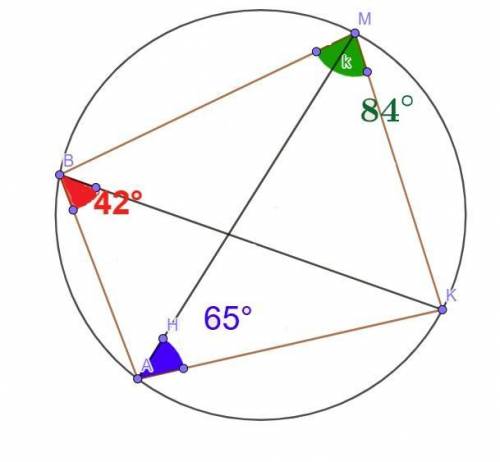
∠А (∠ВАК) = 96°
∠К (∠АКМ) = 73°
∠М (∠ВМК) = 84°
∠В (∠АВМ) = 107°
Объяснение:
Сума протилежних кутів вписаного у коло чотирикутника дорівнює 180 градусам (властивість).
∠ВМК+∠ВАК = 180°
∠ВАК = 180° - ∠ВМК = 180° - 84° = 96°
∠АВК та ∠АМК - вписані кути. Вони спираються на дугу АК.
Вписані кути, що спираються на одну дугу, рівні. ⇒
∠АМК = ∠АВК= 42°
Так як сума кутів трикутника дорівнює 180°, то з ΔАМК знаходимо кут ∠АКМ:
∠КАМ+∠АМК+∠АКМ = 180°
∠АКМ = 180°- ∠КАМ-∠АМК= 180°-65°-42°= 73°
Так як Сума протилежних кутів вписаного у коло чотирикутника дорівнює 180 градусам, маємо:
∠АВМ + ∠АКМ = 180°
∠АВМ = 180° - ∠АКМ = 180°- 73° = 107°
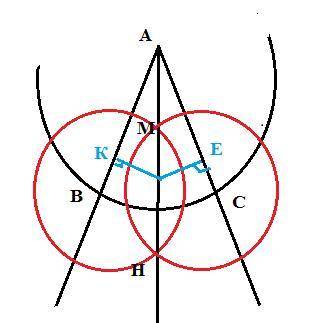
ответ: Это любая точка биссектрисы угла, удаленная на заданное расстояние от вершины.
Объяснение:
Что бы построить биссектрису, надо с центром в вершине угла построить окружность, пересекающую стороны угла (у нас это точки В и С).
Далее, с постоянным раствором циркуля, с центрами в точках В и С построить окружности, пересекающиеся в двух точках ( у нас это точки М и Н. Если через них провести прямую АН, то она и будет биссектрисой.
1. Все точки биссектрисы принадлежат углу, так как углом называется вся часть плоскости, ограниченная сторонами угла (то есть все, что находится внутри сторон.
2. Расстояние от точки до прямой - перпендикуляр от точки к этой прямой. Поэтому получившиеся прямоугольные треугольники АКД и АЕД равны по гипотенузе (АД) и острому углу (биссектриса делит угол пополам). А раз так, то КД=ДЕ, то есть точка Д равноудалена от сторона угла.
3. Ну а заданное расстояние это отрезок АД,
1)треугольник ABD-прямоугольный,т.к. угол А равен 90 градусов,
значит угол BDA=90-36=54,как сумма острых углов прямоугольного треугольника
2)треугольник ABD равен треугольнику ACD по двум катетам или по катету и гипотинузе(как тебе больше нравится),отсюда следует что угол BDA равен углу CAD=54
3)Рассмотрим треугольник AOD
угол CAD=углу BDA=54
а угол AOD=180-54-54=72(как сумма углов в треугольнике)
ответ 72