Если точка делит отрезок в некотором отношении, то проекция точки делит проекцию отрезка в том же отношении (по теореме о пропорциональных отрезках).
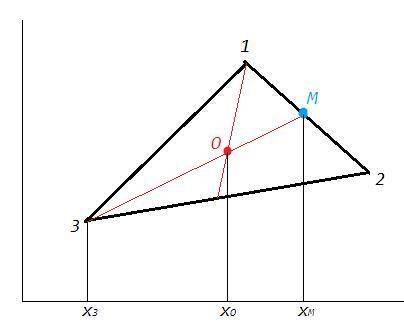
Найдем координату точки M, делящей отрезок 1-2 в отношении 1:1 (пополам, основание медианы)
(xM-x1)/(x2-xM) =1/1 <=>
xM-x1 =x2-xM <=>
2xM= x1+x2 <=>
xM= (x1+x2)/2
Найдем координату точки O, делящей отрезок 3-M в отношении 2:1 (медианы точкой пересечения делятся в отношении 2:1 от вершины)
(xO-x3)/(xM-xO) =2/1 <=>
xO-x3 =2xM-2xO <=>
3xO= 2xM+x3 <=>
xO= (2xM+x3)/3
xO= (2(x1+x2)/2 +x3)/3 =(x1+x2+x3)/3
Аналогично yO= (y1+y2+y3)/3
1) xO= (3-1+1)/3 =1; yO= (1+4+1)/3 =2
2) xO= (-2+5-3)/3 =0; yO= (3-2-1)/3 =0
"Боковые рёбра пирамиды равно наклонены к плоскости основания"
Отсюда следует что точка D находится над центром описанной окружности основания.
У прямоугольного треугольника центр описанной окружности посредине гипотенузы. АВ
Найдем АВ = ВС / sin (A) = 10 / 0.5 = 20
AC = √ (20^2- 10^2) = 10 √3
Пусть С - начало координат
Ось X - CB
Ось Y - CA
Ось Z - перпендикулярно АВС в сторону D
Координаты точек
А ( 0; 10√3; 0 ) он же вектор СА
В ( 10; 0;0)
D ( 5 ; 5√3; 5)
Вектор DB (5;-5√3;-5)
Косинус Искомого угла
| СА * DB | / | CA | / | DB | =
150 / 10√3:/ √( 25+75+ 25) = 3/ √15 = √(3/5)