Объяснение:
М-середина АВ, N -середина АС-по т. о средней линии MN=1/2ВС;
М-середина АВ, К -середина ВС-по т. о средней линии MК=1/2АС;
N -середина АС, К -середина ВС-по т. о средней линии NК=1/2АВ;
ΔАВС∼ ΔMNK по трем пропорциональным сторонам:
АС/MК=1/2, ВС/MN=1/2, АВ/NК=1/2 ⇒к=1/2.
По т. об отношении периметров подобных треугольников
S(АВС)/S(MNK)=к² ⇒ S(АВС)=52кв.ед.
ΔMNK=ΔМКВ по 3 сторонам: МК-общая, МВ=NК=1/2АВ, MN=ВК=1/2ВС ⇒S(MNK)=S(МКВ).
S(АMКN)=S(АВС)-S(MВК)=52-13=39(кв.ед.)
10 см
Объяснение:
Задание
Найти гипотенузу прямоугольного треугольника, если его площадь равна 30 см², а высота, проведённая к гипотенузе, равна 6 см.
Решение
Площадь треугольника равна половине произведения любой его стороны на высоту, проведённую к этой стороне (либо к её продолжению).
Гипотенуза - это одна из сторон треугольника, поэтому площадь можно выразить следующим образом:
S = c · h : 2,
где с - гипотенуза,
h - высота, проведённая к гипотенузе.
Подставим в эту формулу исходные данные и найдём с:
30 = с · 6 : 2
с = 30 · 2 : 6 = 60 : 6 = 10 см.
ответ: гипотенуза равна 10 см.
Пусть х - первое число, у - второе число, тогда:
x²-y²=64
x+y=32
Составим систему из двух известных уравнений :
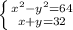
Решим систему методом подстановки, выразив второе уравнение через х:
х = 32 - у и (32-у)²-у2 = 64
1024 - 64у + у² - у² = 64
-64у = 64 - 1024
-64у = 960
у = -15
х = 32 - (-15) =
=32+15 = 47
ответ: первое число - 47
второе число - -15
ABC — равносторонний треугольник, точки M, N и K — серединные точки сторон. Площадь треугольника MNK равна 13 кв. ед. изм.
ОпределИ площадь четырёхугольника AMKC .
решение : Ясно M , K ∉ [AC] ⇒ N ∈ [AC] ) , M ∈ [AB] , K ∈ [BC]
AMKN и CKMN параллелограмм (теорема о средней линии)
ΔAMN = ΔKNM = ΔNKC ⇒ S(AMKC) =3*S(MNK) =3*13 =39 (кв. ед. изм).
ответ : 39(кв. ед. изм).