АД =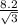 
Периметр ΔАОД = 8,2√3
Объяснение:
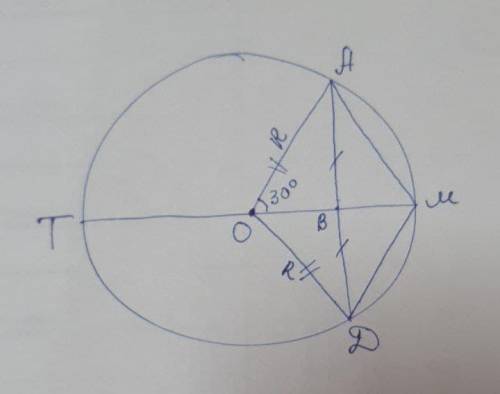
ΔАОД - равнобедренный (ОА=ОД=R), т.к. АВ=ВД (В - середина АД), то ОВ - медиана. Медиана в равнобедренном Δ является также высотой ⇒ОМ⊥АД.
Четырёхугольник АОДМ: Диагонали перпендикулярны, а если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов его противолежащих сторон равны:
АО²+ДМ²=ОД²+АМ²
АО=ОД=R ⇒ R²+ДМ²=R²+АМ²
⇒ДМ=АМ ⇒ Четырёхугольник АОДМ - ромб,
ОА=ОД=ДМ=АМ=R
Рассмотрим ΔАОВ(∠В=90°). ОВ=1/2ОМ (св-во диагоналей ромба)
ОМ=1/2 ТМ ⇒ ОВ=1/4 ТМ = 1/4* 16,4 = 4,1 см
∠О=30°.
ОА=R=ОВ/cos 30° =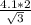 
=
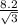
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
АВ=1/2 ОА = 1/2 * =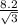 
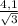, т.к. В - середина АД, то
АД = 2*АВ=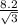
Периметр ΔАОД = 2*ОА+АД= 2*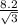 + 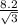= 8,2√3
a)
В единственной картинке.
b)
Так как хорда SF — равна радиусу, то треугольник OFS, образованный двумя радиусами и хордой SF — правильный.
То есть: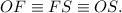
HL — диаметр, перпендикулярный хорде SF, то есть: OM ⊥ SF.
То есть отрезок OM — высота, проведённая к основанию, а в правильном треугольнике, высота, биссектриса и медиана, проведённые к основанию — одно и то же.
То есть OM — медиана, что и означает, что:
Вывод: FS = 16.4см.
c)
Так как OM — высота треугольника OFS, проведённая к основанию, то треугольники OFM & OSM — прямоугольные, так как каждый из них имеет прямой угол (<OMF; <OMS).
OF — гипотенуза, FM — катет, чтобы найти второй катет, то есть OM, используем теорему Пифагора:
Диаметр равен половине отрезка OM, то есть: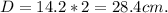
Вывод: Диаметр HL равен 28.4см.
d)
Как я говорила ранее — треугольник OSF — правильный, то есть все стороны равны, то есть:
Вывод: Периметр треугольника OSF равен 49.2см.