Площадь трапеции равна произведению её высоты на полусумму оснований ( среднюю линию).
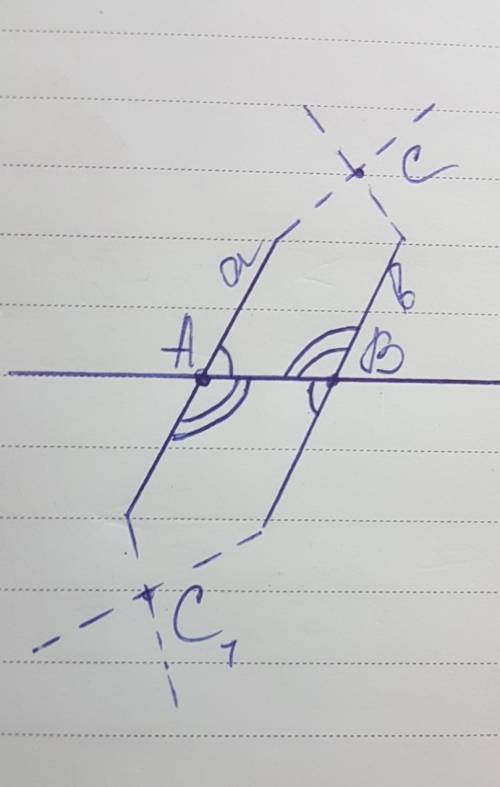
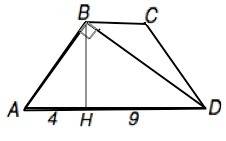
Обозначим трапецию АВСD, высоту - ВН. Тогда АН=4, DH=9
Высота равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности оснований, больший – их полусумме. ⇒
S=BH•HD
Треугольник АВD- прямоугольный.
Его высота – общая с высотой трапеции.
Высота прямоугольного треугольника, проведенная из прямого угла - среднее пропорциональное между отрезками, на которые она делит гипотенузу.
ВН²=АН•DH=4•9=36
BH=√36=6
S(трап)=6•9=54.
запишем отношения для масс подобных частей.
m2/m=(2/3)^3
где m-масса целой пирамиды
m масса части пирамиды с высотой 2/3 считая от вершины.
масса нижней части равна
m*(1-8/27)=m*19/27=27*19/27=19 кг