Периметр прямоугольника равен удвоенной сумме двух его смежных сторон. P = 2(AB+BC),
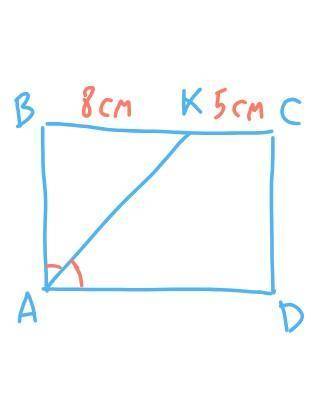
BC = BK + KC = 8 см + 5 см = 13 см.
AK — биссектрисса угла A, угол BAK = угол KAD = 90°÷2 = 45°,
Рассмотрим треугольник ABK. Сумма углов треугольника равна 180°. угол BKA = 180° – угол ABK – угол BAK = 180° – 90° – 45° = 45°, угол BKA = угол BAK, углы при основании равны, треугольник — равнобедренный, значит боковые стороны равны, AB = BK = 8см.
P = 2(AB + BC) = 2(8см + 13см) = 2 × 21 см = 42 см.
ответ: 42 см

∠С=68°, ∠Е=22°
Объяснение:
1)Внутренний угол ΔСАЕ - ∠С смежный с внешним ∠ЕСR=112°
Сумма смежных углов равна 180°⇒∠С=180-112=68°
2) В прямоугольном треугольнике сумма острых углов равна 90° (у прямоугольного треугольника один угол =90°, остальные два острых) ⇒
∠Е=90-68=22°