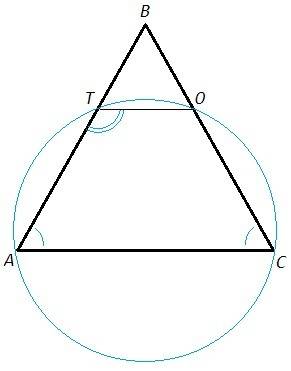
Четырехугольник ATOC является равнобедренной трапецией (TO||AC, ∠A=∠C). Около равнобедренной трапеции можно описать окружность.
Около четырехугольника можно описать в окружность только тогда, когда сумма его противоположных углов равна 180. (Противоположные углы вписанного четырехугольника опираются на дополнительные дуги. Дополнительные дуги составляют окружность, 360. Вписанный угол равен половине дуги, на которую опирается. Сумма противоположных углов вписанного четырехугольника равна 180.)
В трапеции сумма углов, прилежащих боковой стороне, равна 180. (Сумма односторонних углов при параллельных равна 180.) В равнобедренной трапеции углы при основаниях равны, следовательно сумма противоположных углов также равна 180 и около равнобедренной трапеции можно описать окружность.
Объяснение:Пусть АВСД - данный прямоугольник, точка О - произвольная точка внутри прямоугольника.
Выразим периметр прямоугольника:
Р(АВСД) = (АВ + ВС) * 2 = 24; АВ + ВС = 12.
Проведем четыре перпендикуляра от точки О до сторон прямоугольника:
ОЕ (Е принадлежит ВС), ОМ (М принадлежит СД), ОК (К принадлежит АД и ОР (Р принадлежит АВ).
Сумма расстояний от точки О до сторон прямоугольника будет равна:
ОЕ + ОК + ОМ + ОР.
Так как ОЕ и ОК - два перпендикуляра к параллельным сторонам, проведенные из одной точки, значит, Е и К лежат на одной прямой. Получается, что ЕК параллельно ВС и ЕК = ОЕ + ОК = АВ.
Так как Р и М также являются двумя перпендикулярами в параллельным сторонам, то РМ = ОР + ОМ = ВС.
Следовательно, ОЕ + ОК + ОР + ОМ = АВ + ВС = 12 (см).
ответ: сумма расстояний от точки до прямой равно 12 см.
трикутник називається рівнобедрений