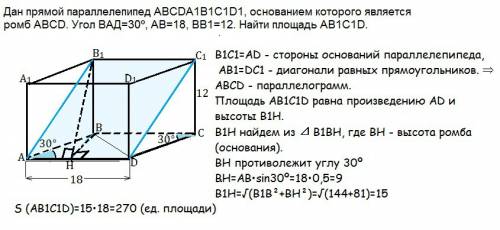
Дан прямой параллелепипед АВСDА1В1С1D1, основанием которого является ромб АВСD. Угол ВАD=30º, АВ=18, ВВ1=12.
Найти площадь AB1C1D.
––––––––––
В прямом параллелепипеде все ребра перпендикулярны основанию, а грани - прямоугольники.
В четырехугольнике AB1C1D стороны В1С1и АD равны как стороны оснований параллелепипеда,
АВ1=DС1 - диагонали равных прямоугольников. ⇒
АВ1С1D - параллело1грамм,т.к. его противоположные стороны равны и параллельны.
Площадь AB1C1D равна произведению АD и высоты, проведенной к АD.
Высота ромба BH - проекция наклонной В1Н на плоскость ромба.
ВН ⊥ АD ⇒
по теореме о 3-х перпендикулярах В1Н⊥ АD и является высотой АВ!С1D
По т.Пифагора из ⊿ В1ВН
B1H=√(B1B²+BH²)
В ромбе высота ВН противолежит углу ВАD=30º
ВН=АВ*sin30º=18*0,5=9
B1H=√(144+81)=15
S (AB1C1D)=15•18=270 (ед. площади)
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Поэтому h²=9·16=144
h=12
Из треугольников. на которые высота поделила искходный треугольник, по теореме Пиагора найдем катеты:
1)9²+12²=225
√225=15
2)16²+12²=400
√400=20
Катеты равны 15см и 20 см,
гипотенуза 9+16=25 см
Можно применить для решения другую теорему.
Катет прямоугольного треугольника есть среднее пропорциональное между
гипотенузой и проекцией этого катета на гипотенузу.
Найдем гипотенузу:
9+16=25 см
Пусть меньший катет будет х.
Тогда его проекция - 9см:
х²= 9·25=225
х=15 см
Больший катет пусть будет у:
у²=25·16=400
у=20 см