Чтобы найти высоты и радиусы, нужно знать площадь треугольника (по формуле Герона)
Полупериметр: (11+13+20)/2 =44/2=22 см
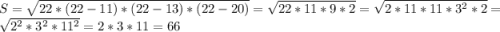
1))) Площадь также находится по формуле:
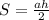
Подставим все известное и тем самым найдем высоту (вместо а будем вставлять все стороны Δка по очереди)
11х/2=66
11х=132
х=12
13х/2=66
13х=132
х=132/13
х≈10,...
20х/2=66
20х=132
х=6,6
Наименьшая высота: 6,6 см.
2))) Площадь также находится по формуле:
р*радиус круга, вписанного в Δ.
Поэтому, радиус = 66/22= 3 см
3))) Площадь также находится по формуле:
аbc/4R, где R - радиус круга, описанного около треугольника.
Радиус: 11*13*20 / 4*х = 66
11*13*5 / х = 66
66х = 11*13*5
х = 11*13*5 / 66
х = 13*5 / 6
х= 65/6 или 10 ц 5/6 см.
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.