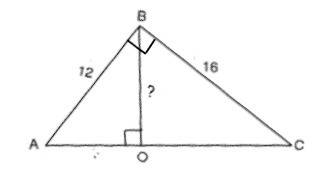
По т.Пифагора найдём гипотенузу.
АС=√(BC²+AC²)=√(256+144)=20 см
Высоту BO проще всего найти из площади треугольника.
S=BC•AB/2
S=BO•AC/2 Следовательно,
BC•AB=BO•AC, откуда
BO=BC•AB:AC
BO=16•12:20=9,6 см
-----
Вариант решения ( несколько длиннее) - его алгоритм дан ниже.
1) Находим гипотенузу по т.Пифагора
2) Катет прямоугольного треугольника – среднее пропорциональное между гипотенузой и проекцией этого катета на неё. ⇒
АВ²=АС•АО, ⇒ АО=АВ²:АС Отрезок СО находим вычитанием АО из гипотенузы или тем же что АО.
3) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. ⇒
ВО²=СО•АО. Вычисления дадут ту же длину ВО=9,6 см
1. По Пифагору квадрат второго катета равен 36²-12²=(36-12)*(36+12)=24*48
И этот же квадрат катета равен произведению гипотенузы на искомую проекцию этого катета на гипотенузу, поэтому проекция равна 48*24/36=8*24/6=8*4=32/см/
2. Площадь треугольника АВС равна половине произведения АВ и АС на синус 45°, т.е. 5√2*8*(√2/2)/2=20
средними линиями мы разбиваем треугольник на четыре равных, а значит, и равновеликих, т.е. с равными площадями. поэтому искомая площадь 20/4=5/см²/
4. формулы параллельного переноса
х'=x+a
y'=y+b
0=3+a⇒a=-3
6=2+b⇒b=4
Пусть С(х;у)
х+а=-3
у+b=2, подставим а и b для точек С и D, получим
х+(-3)=-3⇒х=0
у=-4+2=-2
D(0; -2)
вроде бы так)) надеюсь правильно))