Объяснение:
Фигура называется симметричной относительно некоторой точки (О), если для каждой точки фигуры симметричная ей точка относительно данной точки (О) также принадлежит этой фигуре.
Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1. Точка О считается симметричной самой себе.
* * *
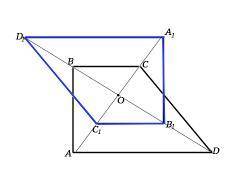
Для построения трапеции, симметричной данной, продолжим в обе стороны от т.О диагонали исходной трапеции.
На продолжении прямой АС отложим ОА₁=ОА, на продолжении прямой DB отложим ОD₁=ОD. Соединим полученные точки вершин фигуры. Четырехугольник А₁В₁С₁D₁ симметричен четырехугольнику ABCD относительно точки пересечения диагоналей - точки О.
Ну вроде как площадь находится формулами S = 4пR квадрат
R для каждого шара свой это 12 и 18, П - это постоянная 3,14
Можно сначала найти площадь каждого шара 4 * 3,14 * 12 в квадрате + 4*3,14*144= 1808,64
Второй шар по той же формуле ответ будет 4069,44
Потом они должны сложится чтобы получилась 1 общая площадь
Объём находится по формуле v= 4\3 (дробь четыре третьих) * П* R в кубе
получаем 4\3 * П * 12 в кубе = 4\3 * П * 1728 = 4\3 * П * 1728 = 2304 * П = 7238,23
Потом то же решение только вместо 12 ставим 18, и складываем