Пусть имеем ромб ABCD, т.O - точка пересечения диагоналей, KO- перпендикуляр плоскости ромба
Рассмотрим прямоугольный треугольник AOD.
AD=46
3*OD=4AO
Пусть x - коэффициент пропорциональности,тогда
AC=4x
OD=3x
(AO)^2+(OD)^2=(AD)^2
(4x)^2+(3x)^2=(45)^2
16x^2+9x^2=2025
25x^2=2025
x^2=81
x=9
то есть
AO=4*9=36
OD=3*9=27
Из треугольника OKD:
(KD)^2=(OD)^2+(OK)^2
(KD)^2=729+1296=2025
KD=45
Из треугольника OKA
(AK)^2=(AO)^2+(KO)^2
(AK)^2=1296+1296=2596
AK=36*sqrt(2)
то есть
KD=KB=45
KA=KC=36*sqrt(2)
Линия пересечения плоскости AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.
Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.
ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:
а)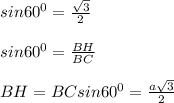
Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.
б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:
в) Найти площадь боковой поверхности - самая простая часть этого задания:
г)