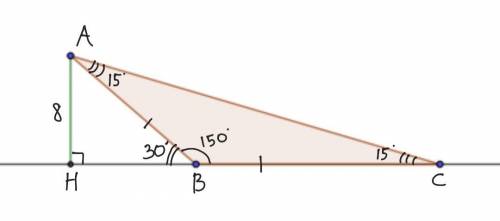
Дано: ΔABC - равнобедренный, АС - основание, АВ=ВС, ∠В=150°, АН - высота, АН = 8 е.д.
Найти: BC.
Решение.
Поскольку треугольник тупоугольный, а высота проведена из острого угла, то высота принадлежит продолжению противолежащей стороны.
Поэтому рисуем продолжение прямой ВС и высоту АН, проведённую к нему.
В ΔАНВ: ∠НВА = 180°-150°= 30° (как смежные).
АНВ - прямоугольный треугольник (АН ведь высота) с гипотенузой АВ.
В прямоугольном треугольнике, если острый угол равен 30°, то противолежащий этому углу катет равен половине гипотенузы.
АН=½АВ.
АВ= 2АН.
АН по условию 8, тогда АВ= 2×8=16.
ΔАВС - равнобедренный, АВ=ВС. Значит, ВС=16 е.д.
ответ: 16 е.д.
Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
В прямоугольном треугольнике катету противолежит острый угол ( прямой противолежит гипотенузе) и сумма острых углов 180°-90°=90°.
Поэтому: если противолежащий катету острый угол одного прямоугольного треугольника равен противолежащем острому углу другого, то прилежащие к равным катетам острые углы также равны
К равным катетам этих треугольников прилежат равные углы: прямой ( по условию) и найденный острый.
Такие прямоугольные треугольники равны по 2-му признаку равенства треугольников, т.е. по стороне и прилежащим к ней углам.
Дано: Решение:
ОАВСD=пирамида рассмотрим треугольник ОВК, где угол К=90
АВСD-ромб по теореме Пифагора ОК=ВО^2-BK^
АС и ВD-диагонали пересек в К OK=169-25=144=12cм
АС=18см: АK=ОK=9см рассмотрим треугольник АОК, где угол К=90
ВD=10см:ВK=OK=5см то теореме Пифагора АО=АК^2+OK^2
ОК=высота AO=81+144=225=15см
ВО=ОD=13см ответ:АО=ОС=15 см.-большее ребро
АО=ОС-?