Теорема о неравенстве треугольника звучит следующим образом:
каждая сторона треугольника меньше суммы двух других сторон.Соответственно подходит вариант 1) вместо углов должно быть сторон.
ответ: 1).→ Задача №4.Применим теорему о неравенстве треугольника. Для этого нужно сравнить каждую сторону с суммой двух оставшихся сторон.
Треугольник №1:
8 см, 2 см, 9 см.
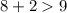- верно.
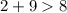- верно.
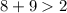- верно.Значит такой треугольник существует.
Треугольник №2:
18 см, 12 см, 14 см.
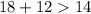- верно.
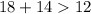- верно.
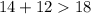- верно.Значит такой треугольник существует.
Треугольник №3:
110 см, 100 см, 90 см.
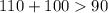- верно.
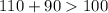- верно.
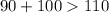- верно.Значит такой треугольник существует.
Треугольник №4:
3 см, 3 см, 7 см.
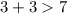- неверно.
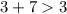- верно.
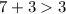- верно.Поскольку в первом случае сумма двух сторон меньше другой стороны, то такого треугольника не существует.
Треугольник №5:
79 см, 40 см, 40 см.
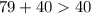- верно.
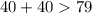- верно.
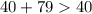- верно.Значит такой треугольник существует.
ответ: 4).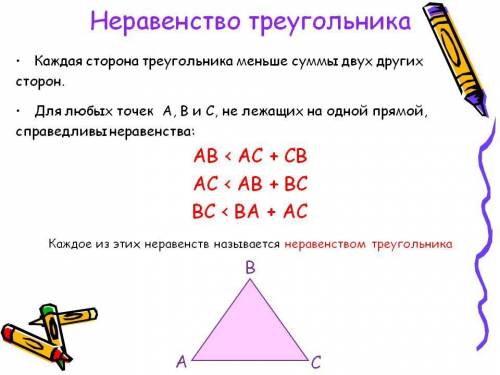
Рассмотрим все случаи неравенства треугольника. Всего 2 случая, НО только один из них верный. Докажем это.
Во-первых, вспомним, что сумма двух сторон треугольника должна быть больше третьей стороны.
Проверим это:
Возьмём случай, где основание нашего равнобедренного треугольника равно 72 см, а боковые стороны по 36 см, ибо они по правилу равны. Проверим, существует ли такой треугольник, следуя теореме (выделена выше наклонным курсивом).
Поскольку первый случай неверный, то такого треугольника не существует.
То есть боковые стороны нашего треугольника равны по 72 см.
(рисунок к задаче прикреплён ниже)
ответ: 5).→ Задача №6.Гипотенуза - самая большая сторона в прямоугольном треугольнике, поэтому она не может равняться в данной задаче
см, поскольку это не самая большая цифра здесь. Получается подходит вариант 5) 11 см, т.к. гипотенуза всегда больше катета.
ответ: 5).