От точки a к прямой а ,проведены перпендикуляр ao и наклонные ab и ac . найдите длины наклонных ab и ac, если ao=15 см , угол c=30°, ac : ab=2: 3 , мне нужна ваша

👇

Ответ:

Aizere20060304

04.01.2022

Рассмотрим тр.AOC (прямоугольный)
в нем угол С равен 30 гр.
згачит угол CAO равен 60 гр. (90-30)
теорема: катет лежащий против угла в 30 градусов равен половине гипотенузы.
так ОА(катет) лежит напротив угла в 30градусов, значит ОА это половина АС(гипотенуза)
таким образом АС=2ОА=30.
АС:АВ=2:3
возьмем 1 часть за х
так, АС это 2х,
АВ это 3х.
получаем уравнения:
1)АС=2х.
2)АВ=3х.
АС=30, значит из 1) находим АС:
30=2х
отсюда х=15.
из 2) находим АВ:
АВ=3х
АВ=3*15
АВ=45.
ответ: АС= 30; АВ=45.

4,4(14 оценок)

Открыть все ответы

Ответ:

Аделя0504

04.01.2022

ответ:

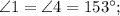
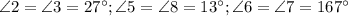№1: $\angle 7$ . №2: $\angle 1 = \angle 4 = 153^{\circ};$ $\angle 2 = \angle3 = 27^{\circ}; \angle 5 = \angle 8 = 13^{\circ}; \angle 6 = \angle 7 = 167^{\circ }$ .

Объяснение:

№1.

Пусть a || b , тогда - секущая.

Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна $180^{\circ}$ .

a || b , по условию.

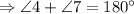
$\angle 4$ и $\angle 7$ - односторонние углы $\Rightarrow \angle 4 + \angle 7 = 180^{\circ}$

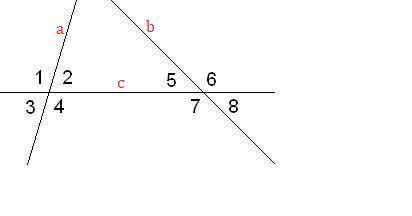
№2.

Обозначим данные прямые буквами 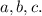a, b, c.

Пусть - секущая прямых и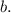

Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".

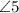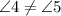$\angle 4$ и $\angle 5$ - накрест лежащие при пересечении и секущей , однако $\angle 4 \neq \angle 5$ .

$\Rightarrow$ и - не параллельны.

============================================================

Свойство: "Вертикальные углы равны".

Свойство: "Сумма смежных углов равна $180^{\circ}$ ".

Рассмотрим углы, образовавшиеся при пересечении прямых и

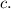
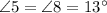$\angle 5 = \angle 8 = 13^{\circ}$ , по свойству вертикальных углов.

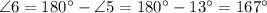$\angle 6 = 180^{\circ} - \angle 5 = 180^{\circ} - 13^{\circ} = 167^{\circ}$ , по свойству смежных углов.

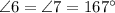$\angle 6 = \angle 7 = 167^{\circ}$ , по свойству вертикальных углов.

===========================================================

Рассмотрим углы, образовавшиеся при пересечении прямых и .

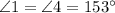$\angle 1 = \angle 4 = 153^{\circ}$ , по свойству вертикальных углов.

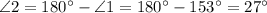$\angle 2 = 180^{\circ} - \angle 1 = 180^{\circ} - 153^{\circ} = 27^{\circ}$ , по свойству смежных углов.

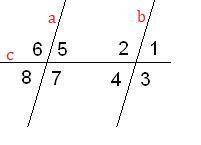
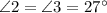$\angle 2 = \angle 3 = 27^{\circ}$ , по свойству вертикальных углов.

1.две параллельные прямые пересекаются с третьей прямой. найди углы, сумма которых с данным углом р

4,4(81 оценок)

Ответ:

Lisakwon

04.01.2022

1)Второй признак равенства треугольников. Теорема. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Третий признак равенства треугольников.

2)периметр - это сумма длин сторон какой-либо геометрической фигуры. Полупериметр - половина периметра.

3)Два треугольника, которые можно совместить наложением, называются равными. ... Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

4)Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведённый из этой вершины к прямой, которая содержит противоположную сторону треугольника. * Прямые, содержащие высоты треугольника, пересекаются в одной точке (которая называется ортоцентром данного треугольника).

Объяснение:

4,7(3 оценок)

Это интересно:

Мир-работы

10.03.2021

Как организовать свое офисное пространство...

Компьютеры-и-электроника

29.01.2021

Как легко изменить свой идентификатор Apple ID...

Мир-работы

19.10.2021

Как отменить собеседование на работу и не потерять репутацию...