незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю незнаю
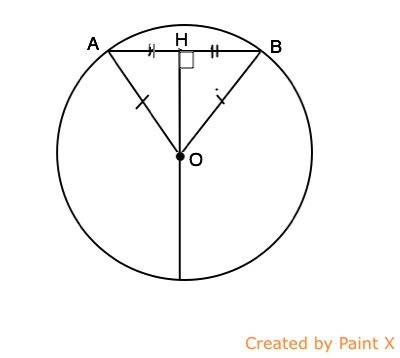
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
Основой прямой призмы является ромб, меньшая диагональ которого равна d. через эту диагональ и вершину верхнего основания проведена плоскость, которая пересекает плоскости двух соседних боковых граней по прямым, угол между которыми равен φ и образует с плоскостью основания угол β. НАЙДИТЕ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПРИЗМЫ
Объяснение:
Пусть меньшая диагональ АС=d. Плоскость сечения пересекает плоскости двух соседних боковых граней по прямым В₁А и В₁С, по условию ∠ АВ₁С= φ. Плоскость сечения образует с плоскостью основания угол β. Это угол ∠В₁ОВ , т.к. ОВ⊥АС ( по св. диагоналей ромба) ВВ₁ перпендикуляр к плоскости ⇒ наклонная В₁О⊥АС.
ОС=1/2*d=0,5 d ( по св. диагоналей ромба). Угол ∠ОВ₁С=φ/2, т.к высота в равнобедренном тр. является биссектрисой.
Δ В₁ОС –прямоугольный : tg (φ/2)=( 0,5 d)/ В₁О, В₁О= d/(2 tg (φ/2).
Δ В₁ВО –прямоугольный : sin β=ВВ₁/ В₁О, ВВ₁= dsin β /(2 tg (φ/2) ;
cos β=ВО/ В₁О , ВО= d/(2 tg (φ/2)* cos β, ВО= d cos β/(2 tg (φ/2).
Δ ОВС- прямоугольный , по т. Пифагора ВС=√ ( ВО²+ОС²),
ВС =d/2 *√ (cos² β/ tg (φ/2)+1)
S(бок. пр.призмы) =Р(осн)*h, h= ВВ₁ , Р(осн)=4*ВС,
Р(осн)=4* d/2 *√ (cos² β/ tg (φ/2)+1)= 2 d√ (cos² β/ tg (φ/2)+1)
S(бок. пр.призмы) = 2 d√ (cos² β/ tg (φ/2)+1)* dsin β /(2 tg (φ/2)=
=2 d² sin β/( √ (cos² β/ tg (φ/2)+1)* tg (φ/2)