Длины диагоналей параллелограмма равны 6 и 8 см, а угол между ними - 60 °. Найдите длины сторон параллелограмма.
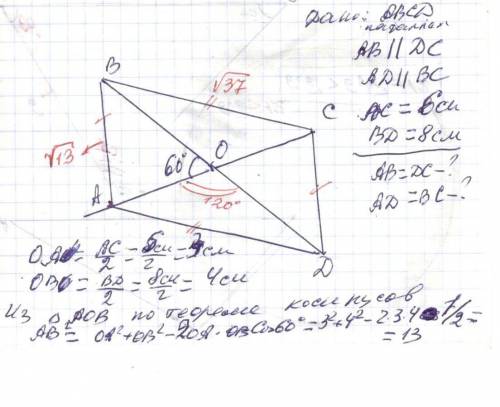
Дано : параллелограмма ABCD (AB || DC ; AD || BC )
AC = 6 см ; BD = 8 см ; α= ∠AOB = 60° .
- - - - - - - - - - - - - -
AB = DC -? AD =BC -?
ответ: √13 см и √37 см .
Объяснение: Из Δ AOB по теореме косинусов :
AB² =OA²+OB² - 2*OA*OB*cosα
Диагонали параллелограмма точкой пересечения делятся пополам
OA =OC =AC/2 = 6 см /2 = 3 см ; OB = OD = BD/2 = 8/2 см = 4 см
AB² =3²+4² - 2*3*4*cos60° =25 -2*3*4*1/2 = 13 (см) ;
AB = √13 см ;
* * * Известно AC²+ BD² =2(AB² +AD²) ⇒ AD = √37 см * * *
Аналогично из Δ AOD :
AD² =OA²+OD² - 2*OA*OD*cos(180° -α )
AD² =3²+4² + 2*3*4*1/2 =25 +2*3*4*1/2 =37 (см) ;
AD =√37 см . * * * ! 6²+8² =2( (√13)²+(√37)² )
x1=12
x2=45
x3=5
Объяснение:
1.так как один угол равен 60 то второй равен 30 а сторона лежащая напротив угла в 30 градусов в прямоугольном треугольнике равна половине гипотинузы, сдедлвательно 6*2=12
2.у равнобедренного треугольника углы при основании равны 1 угол 90 на два других остаётся по 45
3.треугольник равнобедренный так как один угол прямой а второй 45, а в равнобедренном треугольнике высота равна медиане, треугольник поменьше имет уго 45 градусов и прямой следовательно он тоже равнобедренгый следовательно 10/ 2 = 5
В следующий раз обозначай точки буквами
Объяснение:
1.Прямые ВС и АД параллельны(по св-ву паралл-ма) ⇒∠СМД=∠МСВ (как накр. леж. углы при ВС║АД, СМ - секущая)
2. ∠ВСМ=∠МСД(тк СМ-бис-са) ⇒∠МСД=∠СМД
3. Рассмотрим ΔМСД
т.к.∠МСД=∠СМД, то ΔМСД - равнобедренный⇒ СД=МД=11
Р=2АД +2СД (по св-ву парал-ма) Ад=АМ+ДМ=6+11=17
Р=2*17+2*11=56см
ответ:56см