Объяснение:
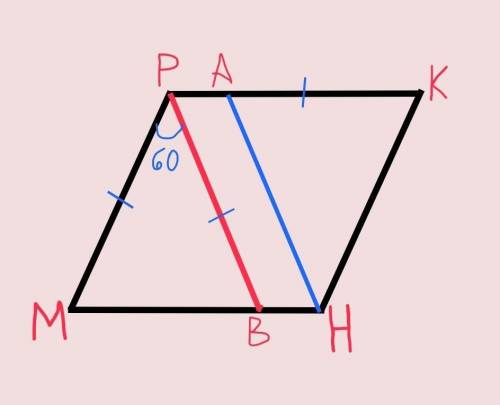
Так как МР=РВ по условию, то ∆МРВ – равнобедренный. Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Тогда угол PMB=угол РВМ=(180°–МРВ)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆МРВ равны 60°, тогда ∆МРВ – равносторонний.
Тогда МВ=МР.
Углы при одной стороне параллелограмма в сумме равны 180°.
Значит угол МРК=180°–угол РМВ=180°–60°=120°
Противоположные углы параллелограмма равны.
Следовательно угол РКН=угол РМН=60°; угол МНК=угол МРК=120°.
МР=АК по условию
МР=КН так как противоположные стороны параллелограмма равны.
Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Следовательно: угол КАН=угол КНА=(180°–угол АКН)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆АКН равны 60°, тогда ∆АКН – равносторонний. Исходя из этого АН=АК
МВ=МР=АК=АН => МВ=АН.
ответ: 1) 60°; 120; 2) равны.
2. Проделав предыдущую операцию на втором конце отрезка (А), получим второй перпендикуляр к прямой АВ. Отложим на полученных перпендикулярах с одной стороны отрезка АВ циркулем отрезки равной длины. Соединив полученные точки, получим прямую, параллельную прямойАВ.
3. Чертим окружность с центром О. Через центр этой окружности проводим прямую а. Продолжаем эту прямую за точку М пересечения с окружностью и на этом продолжении от точки пересечения М откладываем отрезок МА, равный радиусу нашей окружности. Теперь из центра О нашей окружности и из точки конца А, отрезка МА, радиусом, большим радиуса нашей окружности, делаем засечки с обоих сторон прямой. Соединив эти две засечки, получим прямую b, перпендикулярную нашей прямой в точке пересечения ее с нашей окружностью и делящую пополам отрезок ОА, то есть касательную к нашей окружности.
4. На прямой откладываем циркулем отрезок АВ, равный одной из данных сторон. Из точек концов этого отрезка радиусами R и R1, равными длинам двух других сторон проводим засечку (пересечение дуг окружностей этих радиусов). Соединив полученную точку отсечки с концами первого отрезка, получим искомый треугольник.
5. На прямой a откладываем отрезок АВ, равный данной нам стороне. Из точки конца этого отрезка откладываем угол, равный данному α, совместив одну из его сторон с полученным отрезком. На второй стороне угла откладываем отрезок, равный второй данной нам стороне. Соединив точки концов первого ивторого отрезков, получим искомый треугольник.