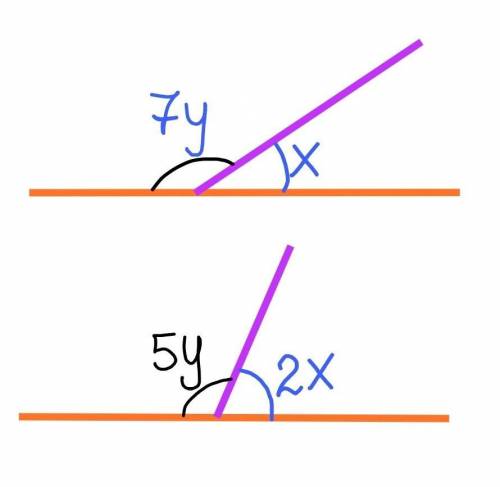
Пусть меньший из данных углов равен х, тогда больший равен 2х. Угол смежный с углом равным х, будет 7у, тогда угол смежный с углом равным 2х, будет 5у.
Смежные углы в сумме равны 180°, тогда получим систему:
Знак системы:
х+7у=180
2х=5у=180
Система:
х=180–7у (Ур 1)
2х+5у=180 (Ур 2)
Подставим значение х из уравнения 1 в уравнение 2, получим:
2(180–7у)+5у=180
360–14у+5у=180
360–180=–5у+14у
9у=180
у=20
Подставим значение у в уравнение 1, получим:
х=180–7*20
х=40
Тогда наменьший из данных углов равен 40°, а другой 40°*2=80°
ответ: 40° и 80°
Дано: AB = 12см
BC = 13см
AC = 20см
A₁B₁ = 9см
Найти: B₁C₁
A₁C₁
По третьему признаку подобия треугольников: Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то они подобны.
Если \frac{AB}{A_1B_1}= \frac{BC}{B_1C_1}=\frac{AC}{A_1C_1}
A
1
B
1
AB
=
B
1
C
1
BC
=
A
1
C
1
AC
, то Δ ABC ~ Δ A₁B₁C₁
Подставим значения сторон треугольника, которые уже знаем
\begin{gathered}\frac{12}{9}= \frac{13}{B_1C_1}=\frac{20}{A_1C_1}frac{4}{3}= \frac{13}{B_1C_1}=\frac{20}{A_1C_1}\end{gathered}
9
12
=
B
1
C
1
13
=
A
1
C
1
20
3
4
=
B
1
C
1
13
=
A
1
C
1
20
Теперь найдём стороны B₁C₁ и A₁C₁
B_1C_1=13:\frac{4}{3}=13*\frac{3}{4}=\frac{39}{4}=9\frac{3}{4}=9,75B
1
C
1
=13:
3
4
=13∗
4
3
=
4
39
=9
4
3
=9,75
A_1C_1=20:\frac{4}{3}=20*\frac{3}{4}=\frac{60}{4}=15A
1
C
1
=20:
3
4
=20∗
4
3
=
4
60
=15
ответ: A₁B₁ = 9см
B₁C₁ = 9,75см
A₁C₁ = 15см
Данный угол sin a = 12/13 он же равен противолежащий катет / на гипотенузу.
Поэтому мы просто подставляем: sin a = 24/x = 12/13 = 24/x, x = 24*13 /12 = 26 см - это гипотенуза.
Через теорему пифагора найдем другой катет, который равен 10 см. значит 1-й катет = 24 см, 2-й катет = 10 см, и гипотенузу т.е 3-я сторона = 26 см