 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 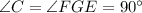 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 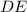 , то
, то 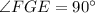 ).
).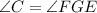 и
и 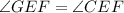 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: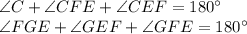
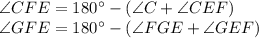
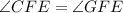 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: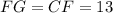
 . Смотрите второй рисунок.
. Смотрите второй рисунок.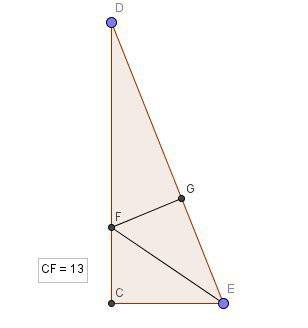
1. На прямой "а" откладываем отрезок АВ, равный отрезку PQ.
2. В точке А строим угол, равный данному, со стороной, лежащей на прямой "а".
3. В точке В строим угол, равный данному, со стороной, лежащей на прямой "а".
4. В точке пересечения сторон построенных углов получаем точку С.
Треугольник АВС построен.
Построение угла, равного данному:
Проводим окружность с центром в точке М - вершине данного угла.
Получим точки К и Н на сторонах данного нам угла.
Проводим окружность этого же радиуса (МН) с центром в точке А.
Получим точку К' на стороне АВ.
Раствором циркуля, равным расстоянию КН из точки К' проведем дугу радиуса КН и получим точку H'.
Через точки А и Н' проведем прямую - угол Н'АК' равен данному нам углу.
Проводим окружность радиуса МН с центром в точке В.
Получим точку К" на стороне АВ.
Раствором циркуля, равным расстоянию КН из точки К" проведем дугу радиуса КН и получим точку H".
Через точки B и Н" проведем прямую - угол Н"BК" равен данному нам углу.
Объяснение:
мне лень было делать на листочке:")