Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
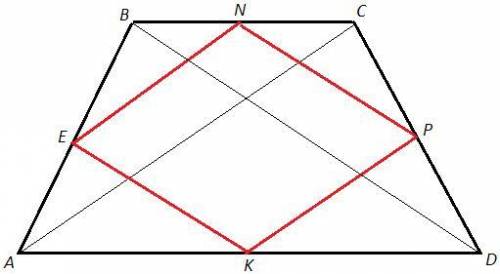
EN - средняя линия в ABC
KP - средняя линия в ADC
EN||AD, KP||AD => EN||KP
Аналогично EK||NP.
ENPK - параллелограмм.
EN=AD/2, EK=BD/2
P(ENPK)= 2(EN+EK) =2(AD/2 +BD/2) =AD+BD
Диагонали равнобедренной трапеции равны.
AD=BD =8
P(ENPK)= 16
Смежные стороны параллелограмма ENPK равны, следовательно он является ромбом.
Середины сторон любого четырехугольника являются вершинами параллелограмма (параллелограмм Вариньона). Периметр параллелограмма Вариньона равен сумме диагоналей четырёхугольника.
1. АВ=√(8²+(-6)²+10²)=10√2
алгоритм - от координат конца отрезка отняли координаты начала. результаты возвели в квадрат, сложили и извлекли корень квадратный из суммы.
2) х=1; у=-1;z=1
алгоритм: сложили соответствующие координаты и поделили каждую на два.
2. 1)АВ(9;-10;7), СВ(4;2;-3) алгоритм : от координат конца отняли координаты начала вектора.
2)IАВI=√(9²+(-10)²+7²)=√230
3) 2АВ+3СВ=2*(9;-10;7)+3(4;2;-3)=(30;-14;5)
2АВ-3СВ=2*(9;-10;7)-3(4;2;-3)=(60;-26;23)
4) IСВI=√(16+4+9)=√29; АВ*СВ/(IАВI*IСВI)=
(36-20-21)/(√230*√29)=-5/√6670≈-5/81.67-0.0612
3. а)-15х-48-27=0⇒х=75/(-15)=-5 скалярное произведение равно нулю.
б)х/(-15)= -4/12= 3/(-9) соответствующие координаты пропорциональны х=5