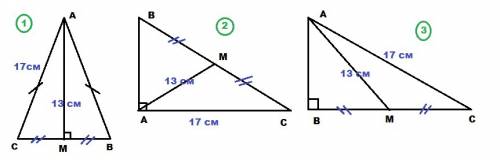
Задача с неполным условием, имеет бесконечно много решений в зависимости от формы треугольника. Рассмотрим три возможных варианта.
1) ΔABC - равнобедренный, AC = AB; AM=13 см; AC = 17 см
AM - медиана, в равнобедренном треугольнике одновременно высота ⇒
CM = MB; AM ⊥ CB
ΔAMC - прямоугольный, ∠AMC=90°; AM=13 см; AC = 17 см
Теорема Пифагора :
CM² = AC² - AM² = 17² - 13² = 120 = (2√30)²
CM = 2√30 см
BC = 2 CM = 2*2√30 = 4√30 см
BC = 4√30 см
=========================================
2) ΔABC - прямоугольный; ∠BAC = 90°; AM=13 см; AC = 17 см
AM - медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
BC = 2 AM = 2*13 = 26 см;
BC = 26 см
====================================
3) ΔABC - прямоугольный, ∠ABC = 90°; AM=13 см; AC = 17 см
AM - медиана ⇒ BM = MC; BC = 2BM
Теорема Пифагора
AB² = AC² - BC² = 17² - (2BM)² = 289 - 4BM²
Теорема Пифагора для ΔABM
AB² = AM² - BM² = 13² - BM² = 169 - BM²
169 - BM² = 280 - 4BM²
3BM² = 111; BM² = 37
BM = √37 см ⇒ BC = 2BM = 2√37 см
BC = 2√37 см
So=√[p*(p-a)(p-b)(p-c)].
В нашем случае р=(13+14+15):2=21.
So=√(21*8*7*6)=84 (по формуле Герона).
Vп=(1/3)*84*24=672см³. (Объем пирамиды)
Объем конуса равен Vк=(1/3)*So*h.
Sok=πr², где r - радиус вписанной в основание (треугольник) окружности.
r=S/p, где S- площадь треугольника, р - полупериметр треугольника.
S=84, p=21 (вычислены выше).
r=84/21=4.
Sok=16π.
Примем π=3.
Тогда Sok=48.
Vk=(1/3)*48*24=384см³. (Объем конуса)
Объем сточенного металла:
Vп-Vк=672-384= 288см³. Это ответ.