медианы в треугольниках пересекаюстся в точке о и делятся в соотношении 1:2.
следовательно медиана выходящая из угла В (назовем ее ВН) = 15.
СН^2=HB^2-CB^2=15^2-12^2=225-144=81. CH=9.
СН- половина АС, т.к. медиана падая на сторону делит ее пополам.
Значит АС=18.
Отсюда найдем АВ по теореме Пифагора.
AB^2=AC^2+CB^2=18^2+12^2=324+144=468.
AB=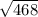 =
= 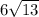
1. Проекция бокового ребра L на основание равна половине диагонали d основания:
d/2=(a/2)*под корнем 2=(9 под корнем 2/2)*под корнем 2=9
Тогда боковое ребро L равно:
L=(d/2)/cos a=9/(под корнем 3/2)=18/под корнем 3=6 под корнем 3.
б) Для этого надо найти апофему А.
А=под корнем(L²-(a/2)² )=под корнем(108-(12/4))=под корнем 270/2=3 под корнем30/2.
Периметр основания: Р=3а=3*9 под корнем 2=27 под корнем 2
Площадь Sбок боковой поверхности пирамиды равна:
Sбок=(1/2)РА=(1/2)*(27 под корнем 2)*(3 под корнем 30/2)=81 под корнем 15/2 кв.ед
Медианы в точке пересечения деляться в отношении 2:1 начиная с вершины..
1) во=10, тогда вв1(медиана)=15
2) по т. Пифогора, в1с=√225-144= √81=9
3) т.к. вв1 медиана, то ав1=в1с, то ас=18
4) по т. Пифогора, ав=√144+324=√468=6√13
ответ: 6√13
пс: я не уверена в последнем действии