Решение задачи указывает на некорректность её условия. Возможно, так и было задумано, чтобы найти в нём ошибку.
———
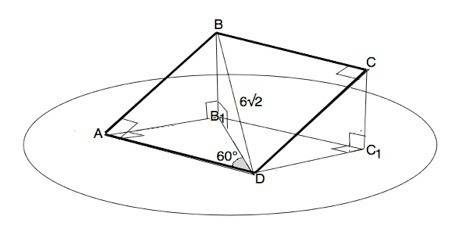
ВВ1 перпендикулярен плоскости альфа, следовательно, этот отрезок перпендикулярен любой прямой, проходящей в этой плоскости через В1.
BD=6√2 по условию.
∆ ВАD- прямоугольный равнобедренный. Его острые углы равны 45°⇒
AD=BD•sin45°=6
По условию AD лежит в плоскости α.
Поэтому по т. о 3-х перпендикулярах В1А⊥AD и C1D⊥DA, и проекция квадрата ABCD на эту плоскость – прямоугольник АВ1С1D.
Угол В1АD - прямой.
Угол В1DА=60°(дано)
Проекция диагонали ВD на плоскость α – В1D и является гипотенузой
треугольника В1АD с прямым углом А.
B1D=AD:cos60°=6:1/2=12 (ед. длины)
———————
Мы получили проекцию наклонной, которая имеет большую длину, чем сама наклонная ВD. Т.е. в прямоугольном ∆ ВВ1D длина катета B1D больше длины гипотенузы BD, чего быть не может.
Но если
а) величина угла В1DА равна 30°,то проекция ВD на плоскост α равна AD:cos30°=4√3.
или
б) угол В1DB=60° - В1D=3√2– тоже допустимый результат.
ответ: a=85, b=105, c=95, d=75
Объяснение: cумма углов треуголника = 360 градусов. чтоб найти отношение надо 360градусов поделить на смму отношений, а затем каждое из отношений умножить на полученный результат. 360:(17+21+19+15)=360:72=5
a=17*5=82
b=21*5=105
c=19*5=95
d=15*5=75