А₁А₂ = 2 см
Объяснение:
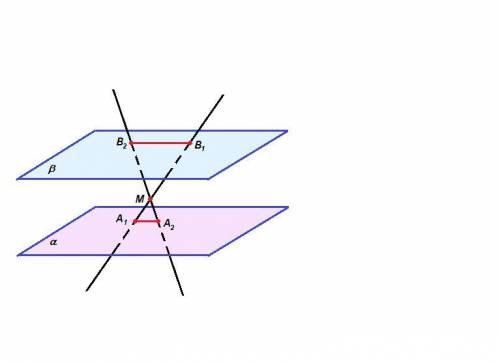
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит
А₁А₂ ║ В₁В₂.
Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,
∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит
ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.
МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см
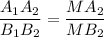
Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,
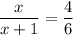
6x = 4(x + 1)
6x = 4x + 4
2x = 4
x = 2
А₁А₂ = 2 см
Основания трапеции параллельны, диагонали трапеции - секущие и при пересечении с ними образуют равные накрестлежащие углы.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. ⇒
∆ ВОС ~∆ АОD по 1 признаку подобия.
СО:ОА=3:7=> ВС:АD=3:7
КН - средняя линия ∆ АВС.
НМ - средняя линия ∆ САD
Отношения сходственных элементов подобных фигур равны. =>
КН:НМ=3:7
КН+НМ=10 частей
10:10=1 см - длина каждой из 10 частей.
КН=3•1=3 см => BС=2•КН=6 см
НМ=7•1=7 см
АD=2•7=14 см