Высоты, проведённые к боковым сторонам AB и BC равнобедренного треугольника ABC, пересекаются в точке M. Прямая BM пересекает основание AC в точке N. Определи ∡ANB.
Нарисуй чертеж ВМ=МС=а AN=ND=b (это обозничили мы так) треугольники APN и MPB подобны с коэффициентом b/a,и высоты тоже
треуг. NQD и CQM подобны с тем же коэфф b/a и высоты тоже. но если у треуг. APN и NQD AN=ND, то и высоты равны. Т.е. точки P и Q находятся на одинаковом расстоянии от AD что и требовалось доказать.
если по поводу высот , что они равны , непонятка, то это следует из того, что отношения высот малого и большого треуг. равно одному и тому же коэффициенту, а сумма этих высот постоянна (высота трапеции)
Объяснение:
3) По теореме Пифагора
АВ²=АС²+СВ²
АВ²=35²+12²
АВ=√(1225+144)=√1369
АВ=37 см
Квадрат катета =произведению гипотенузы на проекцию этого катета
СВ²=АВ*DB
12²=37*DB
DB=144÷37=3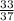
,AD=37-3
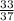=33
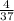
Квадрат высоты = произведению проекций этих катетов
CD²=DB*AD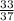=3
*33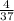
=
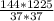, CD=√(
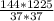)=12*35/37=420/37
8)AB=2+18=20 м
Квадрат высоты = произведению проекций этих катетов
CD²=AD*DB=2*18=36
CD=6 м
Квадрат катета =произведению гипотенузы на проекцию этого катета
AC²=AD*AB, АС=√(2*20)=2√10
По т. Пифагора
АВ²=АС²+АВ², СВ²=АВ²-АС²
СВ²=20²-(2√10)² , СВ=√(400-40)=√360=6√10