Равностороннем треугольнике, сторона которого равна 68 см, соединены середины сторон, в полученном треугольнике опять соединены середины сторон и т. д. (см. рис.).
Вычисли сумму периметров всех треугольников.
Сумма периметров всех треугольников равна
Дополнительные во сторона третьего по порядку треугольника равна
см.
2. Периметр наибольшего треугольника равен
см.
3. Выбери, какую из формул надо использовать в решении задачи:
b11−q2
b11−q
b1(1−qn)1−q
q1−b1
Уравнение окружности имеет вид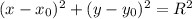
, где 
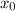и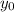 
- координаты центра окружности, а 
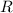- её радиус.
Координаты центра заданной окружности (2; 6).
1. То, что окружность касается оси Ох, значит, что её радиус равен расстоянию от центра окружности до оси абсцисс. На оси Ох ордината равна нулю, а значит, радиус окружности равен 6. Таким образом, уравнение окружности в этом случае:
.
2. То, что окружность касается оси Оy, значит, что её радиус равен расстоянию от центра окружности до оси ординат. На оси Oy абсцисса равна нулю, а значит, радиус окружности равен 2. Таким образом, уравнение окружности в этом случае: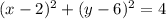
.