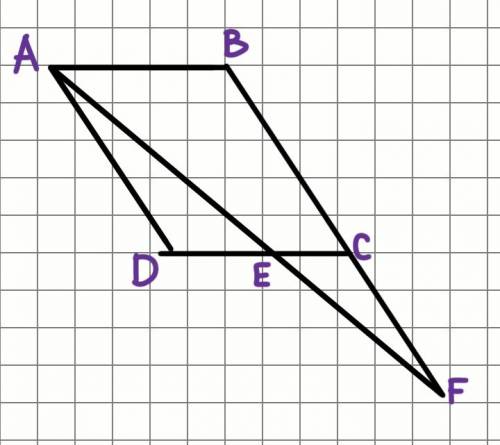
AB и DC параллельны (противоположные стороны параллелограмма).
∠BAF = ∠CEF - соответствующие углы при AB║CD и секущей AF.
∠ABC = ∠ECF - соответствующие углы при AB║CD и секущей BF.
Рассмотрим ΔABF и ΔECF
1. ∠BAF = ∠CEF (из решения)
2. ∠ABC = ∠ECF (из решения)
Отсюда следует, что ΔABF и ΔECF подобны по двум углам.
Найдём коэффициент подобия, он равен отношению подобных сторон треугольников:
k = BF/CF = (56+30)/30 = 86/30 = 43/15
Также из подобия следует, что AB : EC = k
Найдём AB из этой записи:
AB/15 = 43/15
AB = 15*43/15
AB = 43
AB = CD = 43 (так как ABCD параллелограмм)
DE = CD - EC = 43 - 15 = 28
ответ: DE = 28
3. 14см
4. 10+2√3
Объяснение:
3. берём треугольник КLE
угол L =30°, т.к. в треугольнике 180°-90°(прямой угол)и-60°(угол К)
КЕ = 1см (как катет напротив угла 30° равен половине гипотенузы)
RS=LK =2 см (ибо параллельны)
KS=KE+ES=1+4=5
LR=KS (параллельность)
P=LR+RS+SK+KL=5+2+5+2=14cм
4. решаем по такой же схеме.
АД=ВС=3
берем треугольник АДМ(букву М я сама поставила, ибо там пусто)
треугольник АДМ равнобедренный (АД=ДМ)
по теореме косинуса:
угол А равен углу М= (180-60)/2=45°
АМ²=√АД²+ДМ²-2*АД*ДМ*соsуглаД(корень над всем)=√9+9-18*cos60°(=1/2)=√9+9-9=√9=3
АМ=√3
АВ=МВ+АМ=2+√3
ДС=АВ=2+√3(параллельность)
Р=ДС+СВ+АВ+АД=(2+√3)+3+(2+√3)+3=10+2√3