Объяснение:
Дано:
Окружность (O;r)
4-угольник ABCD - вписан в (O;r)
продолж.ВА пересек. продолж. CD в т. К.
Доказать:
∆BКС ~ ∆DКA
Доказательство:
Если 4-угольник можно вписать в окружность =>
=> сумма двух противоположных углов равна 180°:

Обозначим для удобства
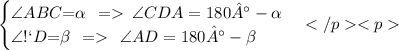
Обратим внимание, что прямые КВ и КС можно расценивать как развернутые (180°) углы: уг.KAB и уг.КDC
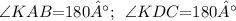
Представив развернутые углы KAB и КDС,как сумму углов, их составляющих
(КАD + BAD и КDA + CDA соответственно) ,
выразим через них углы КAD и КDA:
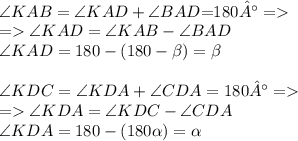
А это означает, что:
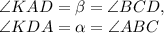
Также, вследствие того что:
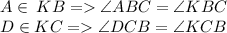
(по сути, АВС и КВС - это один и тот же угол,
DCA и КСА - аналогично).
Рассмотрим ∆BКС и ∆DКA:
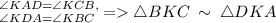
Что и требовалось доказать.
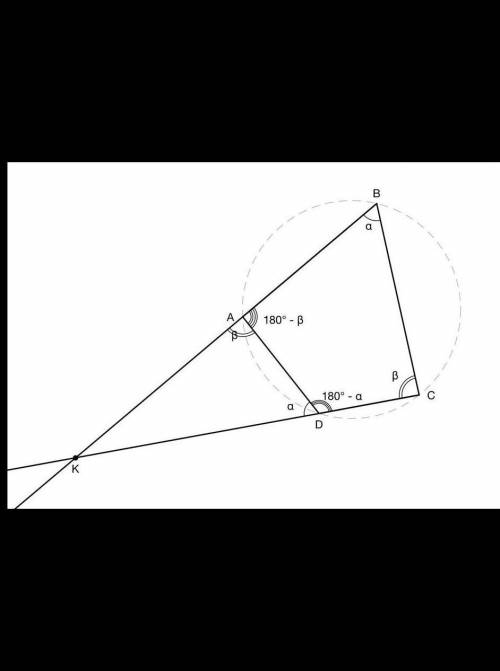
Дан треугольник с вершинами А (-1;4 ), В (-2;-4), С (6;3).
Угол А - это угол между прямыми АВ и АС.
Используем формулу определения тангенса угла между прямыми по их угловым коэффициентам.
Для этого находим угловые коэффициенты к прямых АВ и АС.
А (-1;4 ), В (-2;-4), С (6;3)
к(АВ) = Δу/Δх = (4-(-4))/(-1-(-2)) = 8/1 = 8. Это к_2
к(АС) = (4-3)/(-1-6) = 1/(-7) = -1/7. Это к_1
tg φ = |(к_2 - к_1)/(1 + к_1*к_2)| = |(8 - (-1/7))/(1+8*(-1/7))| = 57.
φ = arc tg 57 = 1,553254267 радиан = 88,99491399°.