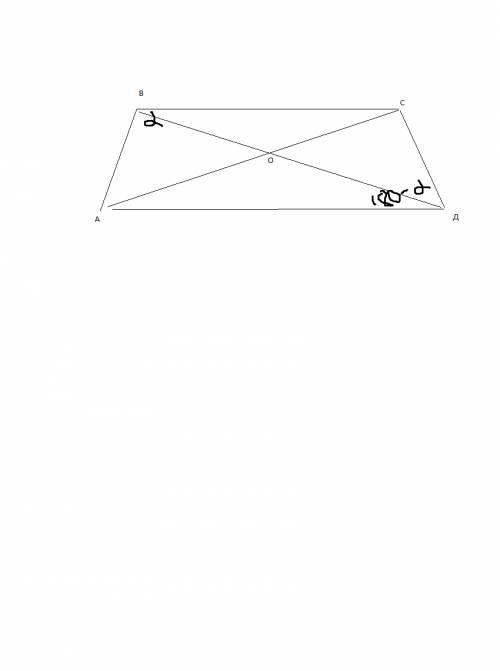
пусть угол АВс равен альфа, тогда АДС - 180-альфа.
У тебя известны ВС=4, АВ=СД=5, АД=6. Тогда ты можешь по теореме косинусов найти диагонали а потом их сумму. Найдем сначала АС. АC^2=AB^2+BC^2-2AB*BC*cosальфа. И с другой стороны это равно СD^2+AD^2-2CD*AD*cos(180-альфа).
Приравниваем. кос(180-альфа)=-косальфа. Этим пользуясь получается 4^2+5^2-2*4*5cosальфа=5^2+6^2+2*5*6cosальфа.
cosальфа=-0.2. АС^2=4^2+5^2-2*4*5*(-0.2). AC^2=49, AC=7. Так же находишь вторую диагональ по теореме косинусов и складываешь. Скорей всего есть в несколько раз короче честно говоря)
а) 9см б) нет
Пошаговое объяснение:
Сначала разберёмся что такое равновеликая и равносоставленная фигура. Равновеликими называются те фигуры, которые равны по площади. Равносоставленные фигуры - это фигуры, которые можно разрезать на одинаковое число попарно равных фигур. Пример равносоставленных фигур смотрите на рис 1.1 и рис 1.2
Приступим к решению:
а) Пусть длина начального прямоугольника а₁, ширина b₁, тогда площадь- S₁. Тогда длина второго прямоугольника а₂, ширина b₂, площадь- S₂. По определению равновеликих фигур можем записать, что их площади равны, и каждая из которых равно произведению длины и ширины:
ответ: ширина второго прямоугольника равна 9 см.
б) Теорема гласит, что любые два равновеликих многоугольника равносоставлены. Но в нашем случае есть и другое условие, а именно: прямоугольники разделили на два треугольника диагональю (см рис 1.3). Полученные треугольники попарно неравные, следовательно равносоставленными их назвать нельзя.
ответ: нет.
Лучший ответ
проводим высоту и из этой же точки диагональ,
находим высоту корень из 25-1=24, 2 корня из 6
далее находим диагональ корень из 24+25=49, 7 сумма диагоналей 14