13
Объяснение:
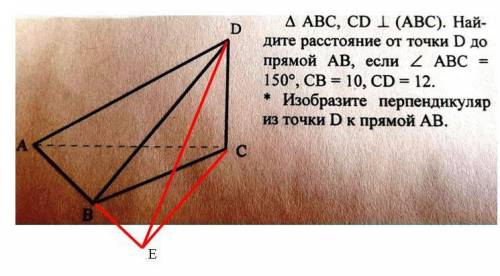
DC⊥(ABC), ∠ABC=150°, CB=10, CD=12
DC⊥(ABC), BC∈(ABC)⇒DC⊥BC
Опустим из точки С перпендикуляр на прямую АВ. Очевидно, то что основание этого перпендикуляра Е будет принадлежать не отрезку АВ , а его продолжению за точку В. Это из-за того что ∠ABC=150°-тупой.
∠СВЕ=180°-∠ABC=180°-150°=30°, ∠СЕВ=90°⇒СЕ=0,5ВС=0,5·10=5
∠DСЕ=90°⇒DЕ²=СЕ²+DС²=5²+12²=169⇒DЕ=13
DC⊥(ABC), Е∈(ABC)⇒отрезок СЕ- орт.проекция отрезка DЕ
CЕ⊥АB⇒DЕ⊥АВ⇒DЕ-отрезок определяющий расстояние от точки D до прямой АВ.
Достоверность требуемого построения доказана по ходу решения задачи.
Рассмотреть треугольник MNC. Отрезок АР в нём - средняя линия, следовательно, точка Р делит сторону NC пополам.
Но NC=3, значит, NP=1,5.
Таким образом, BN относится к NP как 1:1,5 или как 2:3. Поскольку MN и АР параллельны (по построению), то таким же будет и соотношение отсекаемых ими отрезков на стороне АВ.
ответ: 2:3