a = 12 см
b = 16 см
Найдем гипотенузу треугольника по теореме Пифагора:
c = √(a² + b²) = √(12² + 16²) = √(144 + 256) = √400 = 20 см
а) синус большего острого угла треугольника:
больший острый угол лежит против большего катета, т.е. ∠В.
Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе:
sin B = b / c = 16 / 20 = 0,8
б) сумму синусов острых углов:
sin A = a / c = 12 / 20 = 0,6
sin A + sin B = 0,6 + 0,8 = 1,4
в) тангенс одного из острых углов:
тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему:
tg A = a / b = 12 / 16 = 3/4
г) произведение тангенсов острых углов:
tg B = b / a = 16 / 12 = 4/3
tg A · tg B = 3/4 · 4/3 = 1
д) сумму квадратов синуса и косинуса каждого из острых углов:
косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе:
cos A = b / c = 16 / 20 = 0,8
cos B = a / c = 12 / 20 = 0,6
sin²A + cos²A = 0,6² + 0,8² = 0,36 + 0,64 = 1
sin²B + cos²B = 0,8² + 0,6² = 0,64 + 0,36 = 1
е) произведение тангенса и котангенса каждого из острых углов:
котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему:
ctg A = b / a = 16 / 12 = 4/3
ctg B = a / b = 12 / 16 = 3/4
tg A · ctg A = 3/4 · 4/3 = 1
tg B · ctg B = 4/3 · 3/4 = 1
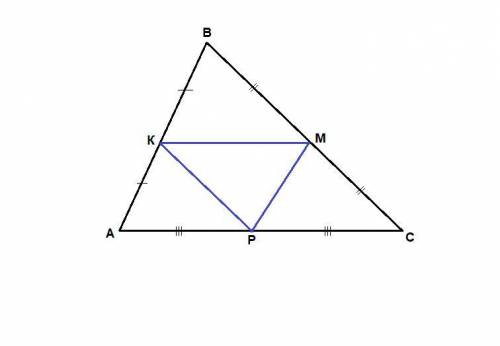
Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.
МР = АВ/2, ⇒
МР = АК = КВ
КР = ВС/2, ⇒
КР = ВМ = МС
КМ = АС/2, ⇒
КМ = АР = РС.
Таким образом ΔАКР = ΔКВМ = ΔРМС = ΔМРК по трем сторонам.
Для ΔАКР и ΔАВС:
∠А - общий,
∠АКР = ∠АВС как соответственные при пересечении параллельных прямых КР и ВС секущей АВ, значит
ΔАКР подобен ΔАВС по двум углам.
Значит треугольнику АВС будут подобны и все остальные треугольники, равные треугольнику АКР:
ΔКВМ подобен ΔАВС
ΔРМС подобен ΔАВС
ΔМРК подобен ΔАВС
1. 13 см. 2. Sполн = 108√3см².
Объяснение:
1. Диагонали ромба делятся пополам. Тогда в прямоугольном треугольнике SOC по Пифагору найдем высоту пирамиды SO. SO = √(SC²-OC²) = √(15²-9²) = 12 см.
В прямоугольном треугольнике SOD по Пифагору найдем гипотенузу SD (меньшую боковую грань пирамиды).
SD = √(SO²+OD²) = √(12²+5²) = 13 см.
2. Пирамида правильная => в основании лежит правильный треугольник, а вершина проецируется в центр треугольника (пересечение высот и медиан - в правильном треугольнике это одно и то же). Двугранный угол при стороне основания - это угол между апофемой (высотой грани) и плоскостью основания, то есть это угол SHO. Тогда в прямоугольном треугольнике SHO угол OSH равен 30 градусов (по сумме острых углов треугольника) и гипотенуза SH = 2·OH (по свойству катета, лежащего против угла 30 градусов). По Пифагору 4·ОН² - ОН² = SO². Или 3·ОН² = 36. =>
ОН = 2√3 см. => SH = 4√3 см. ОН - это 1/3 высоты основания. Высота основания ВН = 3·2√3 = 6√3 см. Сторону основания найдем из формулы высоты основания:
h = (√3/2)·h => a = 2h/√3 = 12 см.
Тогда площадь основания пирамиды равна по формуле:
So = (√3/4)·а² = 36√3 cм². Площадь боковой грани (площадь треугольника) равна
Sг = (1/2)·SH·АC = (1/2)·4√3·12 = 24√3 см². Таких граней три. =>
Sбок = 3·24√3 = 72√3 см². Площадь полной поверхности пирамиды равна
S = So+Sбок = 36√3+72√3 = 108√3см².