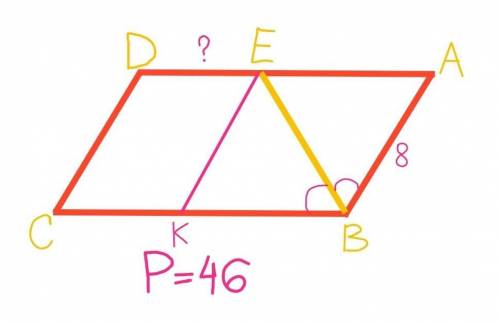
Объяснение:
Из точки Е проведем отрезок ЕК, параллельный АВ.
Противоположные стороны параллелограмма параллельны, тоесть СВ//DE => ЕА//КВ и DE//CK
Так как в четырехугольнике КЕАВ стороны попарно параллельны, следовательно КЕАВ – параллелограмм.
ВЕ – биссектриса угла КВА по условию и диагональ параллелограмма КЕАВ.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Следовательно: КЕАВ – ромб
У ромба все стороны равны. Исходя из этого: ЕА=КВ=АВ=8 см.
СD=AB=8 так как противоположные стороны параллелограмма равны.
Р(АВСD)=АВ+ВС+CD+AD=AB+BK+KC+CD+DE+EA=8+8+KC+8+DE+8=32+KC+DE
Так как Р(ABCD)=46 см по условию, то получим уравнение:
32+КС+DE=46
KC+DE=14 см
Так как ЕК//АВ, а АВ//CD, то ЕК//CD;
DE//CK (доказано ранее);
Исходя из этого: CDEK – параллелограмм.
Противоположные стороны параллелограмма равны, тоесть DE=CK.
Тогда 2DE=14 см
DE=7 см
ответ: 7 см
ABCDA1B1C1D1 куб. В1М - одна сторона сечения (соедини в и М1), В1С - вторая сторона сечения. Грани AA1D1D и BB1C1C расположены в параллельных плоскостях, следовательно, стороны сечения, которые находятся в этих гранях, будут параллельны, т.е. так же будет проходить через середину канта и вершину. Значит MD - третья сторона сечения. Аналогично, ND - четвертая сторона. MB1ND - искомое сечение. Его стороны соединяют вершины грани с серединой кантов, а у куба все грани квадраты, значит все стороны сечения равны.
А1В1=а, тогда А1М=а/2. Сторона сечения МВ1=√(a^2+(a/2)^2)=√(a^2+a^2/4)=√(5a^2/4)=a√5/2
Периметр Р=a√5/2 * 4=2a√5
Вот на 2 во ответ