С линейки и циркуля:
Начерти прямую а и отрезок АВ измерь циркулем расстояние от точки А до отрезка и начерти круг,точно так же поступи с точкой В. Затем на касательных к окружности поставь точки,они тебе и нужны.
Прямой угол меньше тупого угла. Поэтому высота тупоугольного треугольника, проведенная из вершины острого угла, всегда расположена вне самого треугольника и пересекает не саму сторону, к которой проведена, а её продолжение. Об этом важно помнить.
В равнобедренном треугольнике АВС углы при основании АС равны по (180°- ∠АВС):2=(180°-112°):2=34°
АF- биссектриса. Поэтому ∠FAC=∠BAF= ∠ BAC:2=34°:2=17°
Из суммы углов треугольника
∠BFA=180°-∠BAF-∠ABF=180°-17°-112°=51°
Сумма острых углов прямоугольного треугольника 90° ⇒
∠НАF=90°-51°=39°
Объяснение:
Площадь круга, как Вы помните, находят по формуле
S=πr²
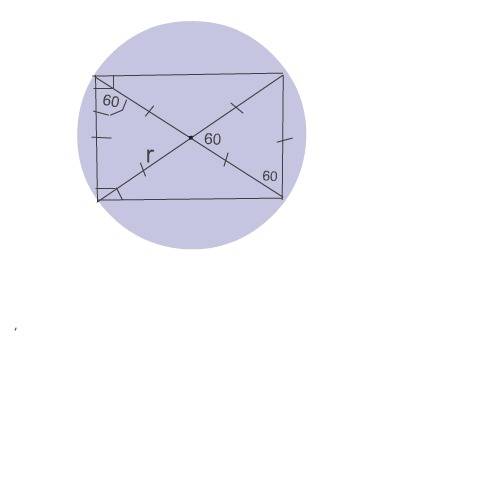
Радиус находим из остроугольных треугольников, образовавшимися диагоналями при меньшей стороне прямоугольника.
Эти треугольники - равносторонние, т.к. угол при пересечении диагоналей равен 60°, а сами диагонали делятся пополам и этим образуют равнобедренные треугольники, углы которых при основании, равном меньшей стороне вписанного прямоугольника, тоже равны 60°.⇒cледовательно, каждая половина диагонали равна меньшей стороне прямоугольника. А так как диагонали здесь являются диаметрами окружности, то радиус описанного круга тоже равен меньшей стороне прямоугольника.
r=10 см
S=πr²,
S=100 π см²
Надо построить перпендикуляр к отрезку, проходящий через его середину. Точка пересечения его с заданной прямой и будет нужная тебе.
Перпендикуляр, к отрезку, проходящий через его середину строится с циркуля и линейки так - проводятся 2 окружности произвольного ОДИНАКОВОГО радиуса, (лишь бы радиус был больше половины отрезка.. можно взять сам отрезок в качестве радиусов) с центрами в концах отрезка. Через точки пересечения окружностей проводится прямая линяя. Она будет перпендикулярна отрезку, будет проходить через его середину и КАЖДАЯ её точка будет равноудалена от концов отрезка. Там, где она пересечет прямую (а), и будет та точка, которая тебе нужна.