Равнобедренный треугольник - это треугольник, в котором две боковые стороны между собой равны.
Свойства равнобедренного треугольника:
в равнобедренном треугольнике углы, лежащие на основании, равны.в равнобедренном треугольнике высота, проведённая к основанию, является медианой и биссектрисой.в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой.в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.Высота - это перпендикуляр, опущенный из вершины треугольника к противолежащей стороне.
Медиана - это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Биссектриса - это луч, соединяющий вершину треугольника с противолежащей стороной и при этом делящий угол на две равные части.
Дан прямоугольный ΔABC с прямым углом B. BO - медиана, проведенная из вершины прямого угла. Опишем около ΔABC окружность. Тогда гипотенуза AC будет являться диаметром окружности, так как вписанный угол ABC является прямым, то он опирается на диаметр окружности.
Медиана в треугольнике является отрезком, опущенным из вершины треугольника на середину противолежащей стороны. BO делит AC пополам. BO соединяет точку на окружности и центр окружности - тч.О, т.е. является радиусом окружности.
Отрезки BO = AO = OC - являются радиусами одной и той же окружности. ⇒ BO = AC/2.
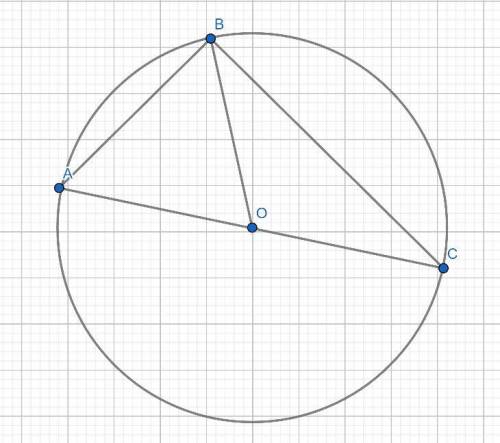
Дан прямоугольный ΔABC с прямым углом B. BO - медиана, проведенная из вершины прямого угла. Опишем около ΔABC окружность. Тогда гипотенуза AC будет являться диаметром окружности, так как вписанный угол ABC является прямым, то он опирается на диаметр окружности.
Медиана в треугольнике является отрезком, опущенным из вершины треугольника на середину противолежащей стороны. BO делит AC пополам. BO соединяет точку на окружности и центр окружности - тч.О, т.е. является радиусом окружности.
Отрезки BO = AO = OC - являются радиусами одной и той же окружности. ⇒ BO = AC/2.

это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием
Объяснение: