ответ: 7/8
Объяснение:
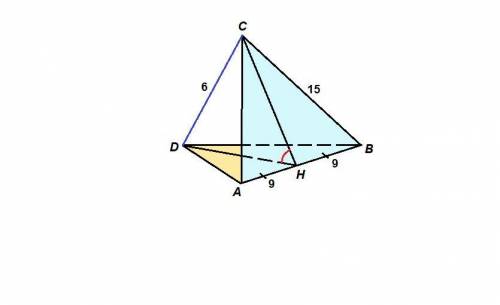
Пусть Н - середина АВ.
СН - медиана равнобедренного треугольника АВС, значит СН - высота, СН⊥АВ.
DH - медиана равнобедренного треугольника ABD, значит DH - высота.
DH⊥AB.
Следовательно, ∠CHD - линейный угол двугранного угла между плоскостями, искомый.
ΔСНВ: ∠СНВ = 90°, НВ = АВ/2 = 9; по теореме Пифагора
СН = √(СВ² - НВ²) = √(15² - 9²) = √(225 - 81) = √144 = 12
DH - медиана, проведенная к гипотенузе прямоугольного треугольника, значит равна половине гипотенузы:
DH = AB/2 = 9
Из ΔCHD по теореме косинусов:
CD² = CH² + DH² - 2 · CH · DH · cos∠CHD
36 = 144 + 81 - 2 · 12 · 9 · cos∠CHD
216 · cos∠CHD = 189
cos∠CHD = 189 / 216 = 7/8
Объяснение:
Чтобы вычислить радиус надо сначала найти длину стороны равностороннего треугольника. Находим по формуле для высоты равностороннего треугольника
h=a√3 /2 отсюда а=2h/√3
A) h=9cm
a=2×9/√3=18/√3см
В) h=36cm
а=2×36/√3=72/√3см
Радиус вписанной окружности для равностороннего треугольника
r=a ÷ 2√3
A) r=18/√3 ÷ 2√3=3см
В) r=72/√3 ÷2√3=12см