ответ: NM= 10см
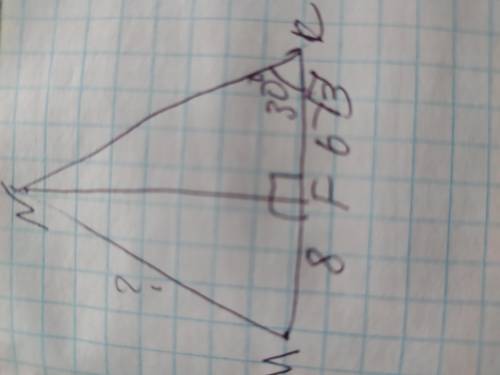
Объяснение: высота NF делит ∆ MNK на два прямоугольных треугольника в которых высота NF является катетом. Рассмотрим полученный ∆NKF. По условиям угол NKF составляет 30°, а катет, который лежит напротив этого угла равен половине гипотенузы. Пусть катет NF будет х, тогда гипотенуза NK будет 2х. Составим уравнение и найдём стороны ∆MKF по теореме Пифагора:
NF²+FK²=NK²
x²+(6√3)²=(2x)²
x²+36×3=4x²
x²+108=4x²
x²-4x²= - 108
- 3x²= - 108
3x²=108
x²=108÷3
x²=36
x=6; сторона NF=6см, тогда гипотенуза NK будет 6×2=12см
Теперь найдём искомую сторону NM по теореме Пифагора, зная MF и NF:
NM²=MF²+NF²
NM=8²+6²=√(64+36)=√100=10см
NM=10см
дано: авс- равнобедренный треугольник.
ам- медиана.(18.4)
р треугольника авм=79.2
найти: р треугольника авс
решение:
ам является и бессектрисой и медианой и высотой (свойства равнобедренного треугольника.)
следовательно: угол а делиться пополам (так как ам является бессектрисой.) следовательно эти половинки ровны.
ам-общая сторона.
ва=ас (по условию так как треугольник авс равнобедренный.)
следовательно треугольники авм=амс (по 1 признаку.)
следовательно р треугольника авс равен.
(79.2-18.4)• 2
все готово