16√3 см²
Объяснение:
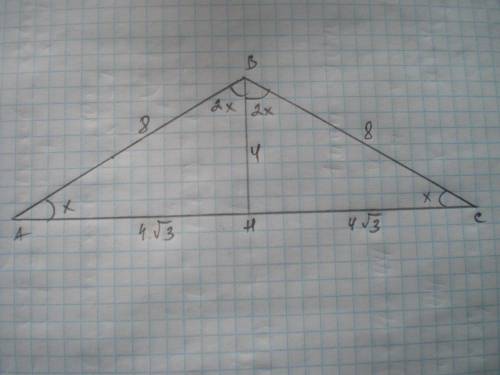
Дано: ΔАВС - равнобедренный, ВС=АВ=8 см.
∠А/∠В=1/4.
Найти S(АВС).
Пусть ∠А=∠С=х° т.к. у равнобедренного треугольника углы при основании равны
Тогда ∠В=4х°.
Проведем высоту ВН, которая является и биссектрисой ∠В по свойству высоты равнобедренного треугольника.
Тогда ∠АВН=1/2 ∠В=2х°
Рассмотрим ΔАВН - прямоугольный, ∠А+∠АВН=90° по свойству острых углов прямоугольного треугольника. Составим уравнение:
х+2х=90; 3х=90; х=30. ∠А=30°, тогда ВН=1/2 АВ = 8:2=4 см по свойству катета, лежащего против угла 30 градусов.
По теореме Пифагора АН=(√АВ²-ВН²)=√(64-16)=√48=4√3 см.
АС=2 АН=4√3 * 2 = 8√3 см
S(АВС)=1/2 * АС * ВН = 1/2 * 8√3 * 4 = 16√3 см²
3. В окружность вписан треугольник ABC так, что АВ - диаметр окружности. Найдите углы треугольника, если: а) ВС=134°
АВ - диаметр - > < C=90 < A=67 (вписанный угол) < B=180-90-67=23
Билет № 3
3. Сумма двух противоположных сторон описанного четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника.
Так как четырехугольник описан вокруг окружности, то сумма других сторон равна 12
S=p*r=(a+b+c+d)*r/2=24*5/2=60
Билет № 4
3. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см. считая от основания. Найдите периметр треугольника.
Дан треугольник ABC. AB=BC. M - точка касания вписанной окружности стороны АВ. N - точка касания вписанной окружности стороны ВC. K - точка касания вписанной окружности стороны АC. AM=3. MB=4.
В соответствии со свойством касательных, проведенных из одной точки к окружности
AM=AK CK=CN BM=BN
P=3+3+4+4+3+3=20