Сторон A B и D E , B C и E F , а также углы B A C и E D F . При каком дополнительном условии можно утверждать, что треугольники A B C и D E F равны? Выберите все правильные варианты ответа. ∠ ∠ B A C — острый ∠ ∠ B A C — прямой ∠ ∠ B A C — тупой ∠ ∠ B C A — острый ∠ ∠ B C A — прямой ∠ ∠ B C A — тупой > A B > B C < A B < B C
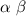 . Тогда
. Тогда 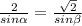
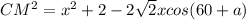
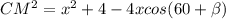
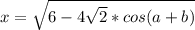
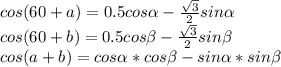
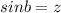
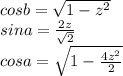
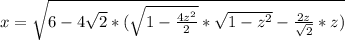
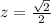
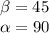
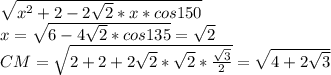
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Поэтому h²=9·16=144
h=12
Из треугольников. на которые высота поделила искходный треугольник, по теореме Пиагора найдем катеты:
1)9²+12²=225
√225=15
2)16²+12²=400
√400=20
Катеты равны 15см и 20 см,
гипотенуза 9+16=25 см
Можно применить для решения другую теорему.
Катет прямоугольного треугольника есть среднее пропорциональное между
гипотенузой и проекцией этого катета на гипотенузу.
Найдем гипотенузу:
9+16=25 см
Пусть меньший катет будет х.
Тогда его проекция - 9см:
х²= 9·25=225
х=15 см
Больший катет пусть будет у:
у²=25·16=400
у=20 см