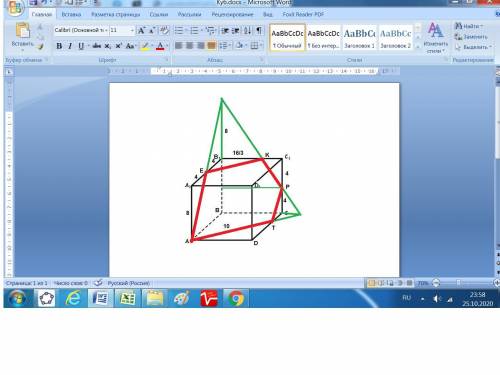
Построено сечение с учётом расположения линий в каждой плоскости.
Длины линий сечения.
AE = √(8² + 4²) = √(64 + 16) = √80 = 4√5.
Длину В1К находим из пропорции (В1К/8 = (8/(8+4)),
отсюда В1К = (8*8)/12 = 16/3.
Тогда ЕК = √(4² + (16/3)²) = √(400/9) = 20/3.
KP = √((8 - (16/3))² + 4²) = √(208/9) = (4/3)√13.
Длину СТ находим из пропорции.
Так как СМ = КС1 = 8 / (16/3) = 8/3, то СМ/СТ = (ВМ/АВ.
Подставим данные. (8/3)/СТ = (8 + (8/3)/8. Получаем СТ = 2.
РТ = √(4² + 2²) = √20 = 2√5.
ДТ = 8 - 2 = 6.
АТ = √(8² + 6²) = 10.
ответ: Р = 4√5 + (20/3) + ((4/3)√13) + (2√5) + 10 =
= 6√5 + (20/3) + ((4/3)√13) + 10.
OB = R = 5 см
АС - хорда
OB ⊥ AC
BD = 2 см
Найти АС
Решение
ОВ = 5 см как радиус окружности
1) Найдём OD
OD = OD - BD = 5см - 2 см = 3 см
OD = 3 см
2) ΔODC - прямоугольный, т.к. по условию OB ⊥ AC, поэтомуможно применить теорему Пифагора.
OD² + DC² = OC²
DC² = OC² - OD²
DC² = 5² - 3² = 25 - 9 = 16
DC = √16 = 4 см
DC = 4 см
3)ΔADO = ΔODC
∠ADO = ∠ODC = 90°
OA = OC = R = 5 см
OD - общая
Из равенства треугольников ΔADO = ΔODC следует равенство
DC = AD = 4 см
А теперь находим АС
АС = 2*4см = 8 см
ответ: 8 см