1)периметр ромба АВСД равен АВ+АД+ДС+ВС=24 см, т.к. у ромба все стороны равны,из этого следует что ВА=АД=ДС=ВС= 24:4= 6см
2)если в прямоугольном треугольнике (ВАО, при ВО- перпендикуляре к АД) катед (ВО равен 3см) в два раза меньше гипотенузы (ВА равной 6 см) то этот катед лежит на против угла равного 30' (угол ВАО равен 30 градусов)
3)Проведем диогональ ромба АС
4)Диогональ ромба является биссектрисой обойх внутренних углов ромба,через которые она проходит, из этого следует что угол ВАС =угол САД=30 градусов :2= 15 градусов и равен углу ВСА и углу АСД
5)треугольник ВАС: угол АВС +угол ВАС+ угол АСБ = 180 градусов, из этого следует что угол АВС=180градусов -(15+15)=150 градусов.
1. Правильный четырехугольник - квадрат.
Диаметр вписанной в квадрат окружности равен стороне квадрата. ⇒ r=d:2=4:2=2 см.
Для описанного вокруг данной окружности треугольника АВС она - вписанная.
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты. Следовательно, высота ∆ АВС =2•3=6 см.
Тогда АВ=ВН:sin60°=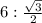 =4√3 см.
=4√3 см.
* * *
2. Для нахождения площади сектора существует формула.
S=Lr:2, где L – длина дуги сектора. ⇒
S=6•4:2=12 см²
Если формула забыта, решить задачу можно без нее.
Длина окружности C=2πr
C=2•p•4=8π см
Площадь окружности S=πr²=16 π см²
Вычислим площадь, которая приходится на сектор с дугой в 1 см.
S:C=16π:8π=2
Тогда площадь сектора
S=2•6=12 см²