Определите косинус угла между треугольником A B1C и плоскостью основания куба ABCDA1B1C1D1 со стороной 1.
Объяснение:
Нужно найти двугранный угол В₁АСВ.
В кубе все грани квадраты. Диагональ квадрата равна √(1²+1²)=√2 , половина диагонали 0,5√2. Пусть О-точка пересечения диагоналей основания.
Диагонали квадрата взаимно перпендикулярны , значит ОВ⊥АС. Тк. проекция ОВ⊥АС ,прямой лежащей в плоскости , то и наклонная В₁О⊥АС. Поэтому ∠В₁ОВ-линейный угол двугранного В₁АСВ.
ΔВВ₁О- прямоугольный , tg∠В₁ОВ=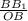
, tg∠В₁ОВ= 
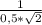=√2.
1+tg²∠В₁ОВ=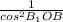
, 1+√2²= 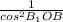,cos∠B₁OB=
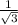, cos∠B₁OB=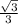
Решение
sin (pi/2+t)-cos(pi-t)+tg(pi-t)+ctg(5pi/2-t) = cost + cost - tgt + tgt =2cost
Объяснение:
sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t). Для упрощения данного выражения используем формулы приведения. По формулам приведения: sin (π/2 + t) = cos t; cos (π - t) = – cos t; tg (π - t) = – tg t; ctg (5π/2 - t) = tg t. Таким образом, мы пришли к выражению: cos t - (– cos t) + (– tg t) + tg t = (раскроем скобки, если перед скобками стоит знак минус "-", то знак слагаемого в скобках необходимо поменять на противоположный) = cos t + cos t - tg t + tg t = (- tg t и tg t взаимно уничтожаются) = 2cos t. ответ: sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t) = 2cos t.